Эффективная ставка формула: Эффективная процентная ставка по кредиту

03.01.1970 alexxlab Comments 0 Comment

Содержание

Эффективная процентная ставка | Формула | Расчет

Определение

Концепция эффективной процентной ставки (англ. Effective Interest Rate) используется для того, чтобы провести оценку всех затрат связанных с привлечением заемного финансирования или доходов от вложений в финансовый актив. Кроме того, требования МСФО (международных стандартов финансовой отчетности) предполагают использование эффективной процентной ставки при оценке финансовых инструментов, учитываемых по амортизированной стоимости, признании расходов и доходов по финансовым инструментам, расчете обесценения финансового актива на основе приведенной стоимости будущих денежных потоков.

Причина использования этой концепции при принятии решений заключается в том, что эффективная годовая процентная ставка может отличаться от номинальной годовой процентной ставки, указанной в договоре. Причиной несовпадения этих величин служат следующие факторы:

количество периодов, за которое в течение года начисляются проценты;

фактическая сумма уплаченных процентов;

фактически понесенные расходы на выплату долга.

Формула

При проведении финансовых расчетов эффективная процентная ставка приводится к годовому формату и также может упоминаться как эффективная годовая процентная ставка или годовая эквивалентная ставка (англ. Annual Equivalent Rate).

Для оценки доходности краткосрочного финансового актива (срок обращения менее 12 месяцев) используется следующая формула:

где i – номинальная годовая процентная ставка, n – количество периодов, за которое в течение года начисляются проценты (например, если проценты начисляются ежемесячно, то n=12).

При оценке стоимости использования краткосрочного финансирования формулу эффективной годовой процентной ставки в общем виде можно записать следующим образом:

r =	Проценты к уплате
	Сумма кредита

В случае дисконтного процента формула должна быть трансформирована следующим образом:

r =	Проценты к уплате
	Сумма кредита — Проценты к уплате

При расчете эффективной процентной ставки также должны быть учтены следующие два фактора:

Дополнительные расходы, которые по сути являются срытыми процентами.

Условия, затрагивающие основную сумму долга. Например, наличие компенсационного остатка по кредиту уменьшает реальную располагаемую сумму.

В этом случае формулы выше должны быть скорректированы следующим образом:

r =	Проценты к уплате + Дополнительные расходы
	Сумма кредита — Компенсационный остаток

Для дисконтного процента следует воспользоваться этой формулой:

r =	Проценты к уплате + Дополнительные расходы
	Сумма кредита — Проценты к уплате — Компенсационный остаток

Примеры расчета

Пример 1

Предположим, что инвестор рассматривает возможность приобретения векселя за $9 655 со сроком погашения наступающим через четыре месяца и номиналом $10 000. В этом случае расчет эффективной годовой процентной ставки будет выглядеть следующим образом.

Проценты к получению = $10 000 — $9 655 = $345

Ставка процента за 4 месяца =	$345	= 3,573%
	$9 655

Эффективная годовая процентная ставка = (1 + 0,03573)^12/4 — 1 = 11,107%

В этом случае мы привели наши расчеты к годовой эквивалентной ставке с учетом концепции сложных процентов.

Пример 2

Компания GFL LTD рассматривает различные варианты финансирования потребности в оборотном капитале в размере $100 000. Существует возможность взять банковский кредит на следующих условиях:

период кредитования 1 год;

номинальная годовая процентная ставка 12%;

единовременная комиссия за рассмотрение кредитной заявки и открытие кредитного счета 2% от суммы кредита;

компенсационный остаток $15 000.

Проценты к уплате = $100 000 × 12% = $12 000

Дополнительные расходы = $100 000 × 2% = $2 000

Эффективная годовая процентная ставка =	$12 000 + $2 000	= 16,471%
	$100 000 — $15 000

Пример 3

Корпорация Tristan Inc. имеет банковский кредит, который был взят на следующих условиях:

сумма кредита $250 000;

период кредитования 1 год;

дисконтный процент при номинальной годовой процентной ставке 15%;

расходы открытие кредитного счета 1% от суммы кредита;

компенсационный остаток $50 000.

Проценты к уплате = $250 000 —	$250 000	= $32 608,70
	(1+0,15)¹

Дополнительные расходы = $250 000 × 1% = $2 500

Эффективная годовая процентная ставка =	$32 608,70 + $2 500	= 20,974%
	$250 000 — $32 608,70 — $50 000

Функция НОМИНАЛ — Служба поддержки Office

В этой статье описаны синтаксис формулы и использование функции НОМИНАЛ в Microsoft Excel.

Описание

Возвращает номинальную годовую ставку, если заданы эффективная (фактическая) ставка и число периодов в году, за которые начисляются сложные проценты.

Синтаксис

НОМИНАЛ(эффект_ставка;кол_пер)

Аргументы функции НОМИНАЛ описаны ниже.

Эффект_ставка. Обязательный аргумент. Фактическая процентная ставка.

Кол_пер. Обязательный аргумент. Количество периодов в году, за которые начисляются сложные проценты.

Замечания

Аргумент кол_пер усекается до целого числа.

Если любой из аргументов не является числом, возвращается #VALUE! значение ошибки #ЗНАЧ!.

Если effect_rate ≤ 0 или < 1, то #NUM! значение ошибки #ЗНАЧ!.

Функция НОМИНАЛ(эффект_ставка,кол_пер) связана с функцией ЭФФЕКТ(номинальная_ставка,кол_пер) через эффективную_ставку=(1+(номинальная_ставка/кол_пер))*кол_пер-1.

Отношение между функциями НОМИНАЛ и ЭФФЕКТ показано в приведенном ниже уравнении.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
0,053543	Эффективная процентная ставка
4	Количество периодов в году, за которые начисляются сложные проценты
Формула	Описание	Результат
=НОМИНАЛ(A2;A3)	Номинальная процентная ставка с условиями, указанными выше	0,05250032

Данные

Описание

0,053543

Эффективная процентная ставка

Количество периодов в году, за которые начисляются сложные проценты

Формула

Описание

Результат

=НОМИНАЛ(A2;A3)

Номинальная процентная ставка с условиями, указанными выше

0,05250032

Функция ЭФФЕКТ — Служба поддержки Office

В этой статье описаны синтаксис формулы и использование функции ЭФФЕКТ в Microsoft Excel.

Описание

Возвращает фактическую (эффективную) годовую процентную ставку, если заданы номинальная годовая процентная ставка и количество периодов в году, за которые начисляются сложные проценты.

Синтаксис

ЭФФЕКТ(номинальная_ставка;кол_пер)

Аргументы функции ЭФФЕКТ описаны ниже.

Номинальная_ставка — обязательный аргумент. Номинальная процентная ставка.

Кол_пер. Обязательный аргумент. Количество периодов в году, за которые начисляются сложные проценты.

Замечания

Значение аргумента «кол_пер» усекается до целого числа.

Если любой из аргументов не является числом, то эффект возвращает #VALUE! значение ошибки #ЗНАЧ!.

Если nominal_rate ≤ 0 или < 1, то #NUM! значение ошибки #ЗНАЧ!.

Функция ЭФФЕКТ вычисляется следующим образом:

Связь функции ЭФФЕКТ(номинальная_ставка;кол_пер) и функции НОМИНАЛ(факт_ставка;кол_пер) выражена уравнением факт_ставка=(1+(номинальная_ставка/кол_пер))*кол_пер -1.

Пример

Данные	Описание
0,0525	Номинальная процентная ставка
4	Количество периодов в году, за которые начисляются сложные проценты
Формула	Описание	Результат
=ЭФФЕКТ(A2;A3)	Фактическая (эффективная) процентная ставка в соответствии с приведенными выше условиями	0,0535427

Данные

Описание

0,0525

Номинальная процентная ставка

Количество периодов в году, за которые начисляются сложные проценты

Формула

Описание

Результат

=ЭФФЕКТ(A2;A3)

Фактическая (эффективная) процентная ставка в соответствии с приведенными выше условиями

0,0535427

Эффективная ставка по кредиту

На заре розничного потребительского кредитования банкиры проводили множество экспериментов с номинальной процентной ставкой по кредитам. Номинальная ставка – это ставка, которая указывается в договоре и на базе которой начисляются проценты за пользование кредитом. Учитывая большие риски розничного кредитования, финансисты закладывали высокую доходность таких программ, и соответственно размер номинальной ставки достигал аж 40-50 % годовых.

Проблема заключалась в том, как показать такую высокую стоимость кредитов потенциальным клиентам. Одни банки попытались быть честными, но естественно, что такие дорогие кредиты у них никто не брал. А вот другие «изобретатели» придумали менее «ужасную» схему ценообразования по кредитам: с использованием ежемесячных и одноразовых комиссий. Путем взимания дополнительных комиссий, банки занижали до приемлемого уровня номинальную ставку и наращивали объемы кредитования.

Потому, когда вы приходите в банк за кредитом, вы должны спросить: «А какая у вашего банка эффективная ставка по кредиту?» И банк должен «раскрыть карты» перед вами.

Давайте разберемся, что такое эффективная процентная ставка и как ее рассчитать?

Естественно, когда мы берем кредит, нас в первую очередь интересует полная его стоимость. Тем более, что нас завлекают слоганами типа «Кредит без переплаты», «10 % по кредиту, 10 дней льготного периода, от 10 тысяч» и т. д. Многие кредитные организации, рекламируя свои услуги, очень часто освещают только вершину айсберга. Когда же мы уже пришли в банк, чтобы воспользоваться «сказочным» предложением, то нас огорошивают суммами дополнительных комиссий и переплат.

Так вот, эффективная процентная ставка по кредиту – это совокупность платежей и комиссий, которую должен выплатить заемщик на протяжении всего кредитного договора. То есть реальная стоимость кредита. Берем ли мы кредит наличными без справок, автокредит, ипотеку…

Расчет эффективной процентной ставки ведется по следующей формуле: номинальная процентная ставка, заявленная банком, плюс комиссии. Что можно отнести к дополнительным банковским комиссиям и платежам: комиссия за рассмотрение заявки по кредиту; комиссия за открытие счета; за обслуживание счета; услуги по страхованию заемщика и его имущества.

При этом единой формулы по расчету все же не существует. Каждый банк предлагает свои условия и вводит свои комиссии. Это право кредитной организации. Но по нашему законодательству любой банк обязан предоставить заемщику всю информацию по платежам и ссудам, которые необходимо оплатить по кредитному договору. И нам необходимо в первую очередь обратить внимание на пункт договора, описывающий эффективную процентную ставку по кредиту.

К сожалению, многие коммерческие банки нередко предлагают нам рассчитать эффективную процентную ставку самостоятельно. Для многих это может быть проблемой. Поэтому прежде, чем взять заем, обязательно просите банковского или стороннего специалиста произвести расчет. Это все должно быть четко прописано. Например, приложение к договору «Уведомление о полной стоимости кредита». Тут все должно быть четко разложено по полочкам. Мы должны видеть, чтобы понимать, сколько заплатим, за что переплатим и сколько. Также банк должен выдать график ежемесячных платежей, в соответствии с которым вы и должны рассчитывать свои средства и возможности.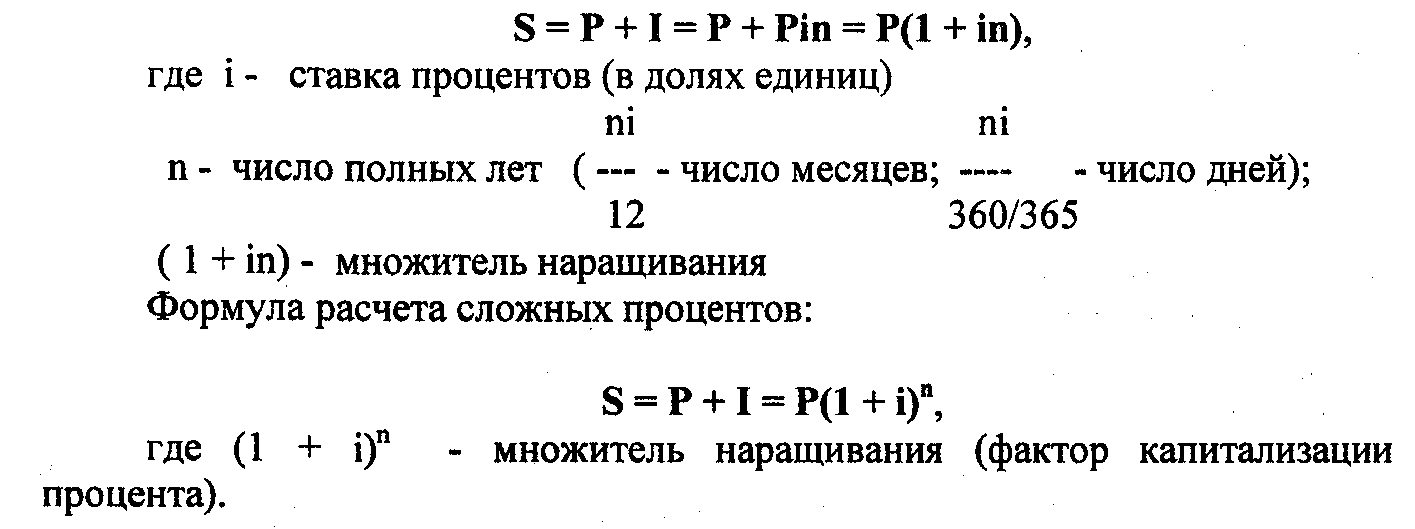

Эффективная, номинальная, реальная ставка по кредиту – отличия

Банк обещает супер выгодные условия, а в результате приходится переплачивать в 2 – 3 раза больше, чем вы ожидали. Знакомая ситуация? Чтобы разобраться, почему так происходит и не попадаться в рекламные ловушки, нужно определить, что такое эффективная, номинальная и реальная ставка по кредиту.

Номинальная процентная ставка

Номинальная ставка – это те цифры, которые банк показывает клиенту в рекламе и пишет крупными символами на сайте.

Что в нее входит

Только непосредственный процент по кредиту

Что в нее НЕ входит

— дополнительные комиссии (за снижение переплаты, за фиксированную переплату и т.д.)

— платежи за обслуживание

— SMS и прочее информирование

— оплата онлайн-банкинга/предоставленной карты (если такие услуги предлагаются)

— оплата страховки

— инфляция

Нужно ли ее принимать в расчет

В любом случае нужно. По итогам анализа банковских предложений в 75% случаев банк с наиболее симпатичным рекламным предложением, в конце концов, окажется выгоднее и по итоговым цифрам.

Главное понимать, что на номинальных цифрах все не закончится, и выплаты заемщики будут учитывать еще массу других финансовых параметров.

При чем тут инфляция

Умные финансовые порталы справедливо указывают, что номинальный и реальный процент отличаются тем, что в первом не учитывается инфляция. Заемщики тут же пытаются применить это к своей практике и понять, что это значит. Условия будут менять каждый год?

Не исключено. Именно для этого обычно предлагается услуга «фиксирования переплаты». Хотя на условия кредитования в равной мере влияют не только инфляционные изменения, но и действия Центробанка, и еще множество параметров.

Тем не менее, согласно действующему законодательству, если в договоре не прописан фиксированный процент, банк имеет право изменить правила в одностороннем порядке и поставить клиента просто перед фактом.

Реальная процентная ставка

Реальная ставка – показатель, с учетом инфляции. Деньги со временем «дешевеют». Данный показатель учитывает инфляционные изменения, демонстрируя насколько действительно вырастает долг по займу или доход при вкладе.

Что в нее входит

Только непосредственный процент, с поправкой на инфляцию

Что в нее НЕ входит

— дополнительные комиссии (за фиксирование/снижение переплат и т.д.)

— платежи за обслуживание

— SMS и прочее информирование

— оплата онлайн-банкинга/предоставленной карты (если такие услуги предлагаются)

— оплата страховки

Нужно ли ее принимать в расчет

Реальная процентная ставка – параметр, больше интересующий вкладчиков. Например, при заявленных 4% доходности, через 3 – 4 года фактическая доходность будет далеко не 4% — ведь деньги подешевеют, и доходность может даже оказаться отрицательной.

Когда это важно для кредита

Этот показатель не фигурирует в кредитных договорах – клиент при желании самостоятельно может рассчитать, как изменилась переплата с учетом инфляции. Но практика свидетельствует о том, что без резких финансовых изменений фактическая переплата со временем дешевеет. Особенно при аннуитетных платежах и долгосрочном кредитовании. Ведь условные 20.000 ежемесячного платежа через 5 – 10 лет будут существенно «дешевле» двадцати тысяч, уплаченных в текущем периоде.

Обычно именно данный пункт является подтверждением определенной выгодности долгосрочных ссуд – цены на желаемый объект (напр. недвижимость) будут расти, а платежи с учетом реальной переплаты с поправкой на инфляцию – «дешеветь». Итоговая переплата таким образом получится достаточно небольшой.

Эффективная процентная ставка (ЭПС)

Эффективная процентная ставка (ЭПС) – это параметр, учитывающий все дополнительные платежи. Ее также называют полной стоимостью кредита (ПСК).

Что в нее входит

— дополнительные комиссии (за снижение/фиксацию переплат и т.д.)

— платежи за обслуживание

— SMS и прочее информирование

— оплата онлайн-банкинга/предоставленной карты (если такие услуги предлагаются)

— оплата страховки

Что в нее НЕ входит

— штрафы

— пени

— изменения условий при перерасчете/рефинансировании

— дополнительные расходы на рефинансирование

Как ее узнать

Согласно распоряжению ЦБ РФ, банки обязаны предоставлять данные по эффективной процентной ставке в открытый доступ.

Но нередко кредиторы обходят данное требование, ссылаясь на индивидуальность расчета. Зайдите на сайт интересующего вас банка и откройте документацию по условиям кредитования. Там будут указаны все «повышающие/понижающие коэффициенты».

Например, + 1% за отсутствие страховки, + 0,5% для ИП и т.д. Повышение/понижение также возможно за определенные суммы/сроки. Выпишите все показатели, которые относятся к вам – и получится «эффективное» значение.

Действительно ли ПСК является полной

Несколько раз заемщики жаловались на то, что полная сумма кредитования не включает все переплаты. ЦБ РФ пояснил, что в данный параметр входят только суммы, которые можно спрогнозировать заранее. Штрафы, пени, изменение при подаче заемщиком заявления на рефинансирование, реструктуризацию – дополнительные параметры, которые в ПСК не учитываются.

Сколько придется платить в конечном итоге

Добросовестные заемщики в течение всего срока кредитования будут платить в соответствии с эффективным ставочным значением (без штрафов/пени).

Перед оформлением договора кредитор обязан предоставить график платежей, по которому также можно высчитать, какой на самом деле будет переплата.

План действий получается следующим:

Выбрать 2 – 3 организации с оптимальным номинальным параметром
Выяснить, каким будет эффективный процент
Принять окончательное решение

Хотите выбрать оптимальный вариант? Обязательно посмотрите:

Материал подготовлен на основе: федерального закона N 353-ФЗ, N351-ФЗ

Понятие, формула и расчет эффективной ставки по вкладу

Банковский вклад является самым востребованным инвестиционным инструментом у граждан нашей страны. Объясняется это пассивным характером подобных вложений и практически отсутствующими рисками. При этом не каждый вкладчик знает, что существует 2 разновидности начисления доходности по открытому депозиту. Это номинальная (исходная, простая) и эффективная ставка по вкладу.

Такое различие становится актуальным в том случае, если речь идет о банковском продукте с капитализацией процентов. В такой ситуации номинальная ставка не будет отражать реальную прибыль, которую в конце срока получит клиент банка. Такую прибыльность можно рассчитать лишь по формуле эффективной процентной ставки.

Понятие и сущность

Эффективная ставка является показателем, используемым при расчетах фактического дохода от инвестиции денег на банковский депозит. Она позволяет учесть капитализацию процентов. Ее значение в каждом конкретном случае будет выше показателя номинальной процентной ставки.

Таким образом, мы можем сделать однозначный вывод, что прибыль, получаемая по вкладу с капитализацией процентов будет выше, чем по тому депозиту, где она отсутствует. Это объясняется тем, что в случае с капитализацией проценты будут начисляться с оговоренной периодичностью и суммироваться к сумме депозита. Такие начисления могут производиться ежемесячно, ежеквартально, ежегодно, а также с любым другим описанным в договоре интервалом.

Зачем на практике ее высчитывать

Мы выяснили, что при помощи эффективной ставки можем вычислить реальную прибыль, которую получим с того или иного депозита. Подобные вычисления могут оказаться незаменимыми при сравнении банковских продуктов от одного или нескольких банков.

Запомните, максимальная доходность достигается при выборе вклада, условиями которого предусмотрена ежемесячная капитализация процентов. Происходит это довольно просто.

После первого месяца оговоренные проценты будут прибавлены к начальной сумме депозита. После второго месяца они будут начислены к значению, сформированному из начальной суммы вклада и процентов по первому месяцу и так далее.

Формула и примеры ее использования

Формула, позволяющая вычислить эффективную ставку по депозиту с ежемесячной капитализацией процентов.

Значение T соответствует сроку размещения вклада в месяцах.

Давайте рассмотрим пример подобного расчета. Предположим, что у нас есть банковский вклад сроком 2 года и номинальной ставкой 10% годовых.

Чтобы получить правильный результат, необходимо учитывать следующий нюанс. Номинальная ставка в приведенном примере составляет 10%. Однако по правилам математических расчетов в формуле используется значение в долях равное 0,1. Посчитать это можно следующим образом: (10%)/(100%)=0,1.

Теперь давайте рассмотрим формулу, которая поможет нам рассчитать эффективную ставку по депозиту с ежеквартальной капитализацией процентов.

Давайте рассмотрим пример такого расчета. Предположим, у нас имеется банковский вклад сроком год и номинальной ставкой 8,25% годовых.

Что изменится, если пополнить или частично снять деньги со вклада

Не секрет, что существуют банковские продукты, которые позволяют производить как пополнение, так и частичное снятие денежных средств с депозита. Естественно, такие действия вкладчика повлияют на итоговую доходность.

Пополняя вклад, клиент банка увеличивает его сумму. Естественно, это приводит к итоговому увеличению дохода.

Снимаю денежные средства с депозита, клиент банка уменьшает его сумму. Естественно, это приведет к итоговому уменьшению дохода.

Определение эффективной годовой процентной ставки

Что такое эффективная годовая процентная ставка?

Эффективная годовая процентная ставка — это реальная доходность сберегательного счета или любых инвестиций с выплатой процентов, если принять во внимание эффекты начисления сложных процентов с течением времени. Он также показывает реальную процентную ставку по процентам по ссуде, кредитной карте или любой другой задолженности.

Ее также называют эффективной процентной ставкой, эффективной ставкой или годовой эквивалентной ставкой.n-1 \\ & \ textbf {где:} \\ & i = \ text {Номинальная процентная ставка} \\ & n = \ text {Количество периодов} \\ \ end {выровнено}
Эффективная годовая процентная ставка = (1 + ni) n − 1, где: i = номинальная процентная ставка = количество периодов

Эффективная годовая процентная ставка

О чем говорит эффективная годовая процентная ставка?

Банковский депозитный сертификат, сберегательный счет или предложение ссуды могут рекламироваться с указанием номинальной процентной ставки, а также эффективной годовой процентной ставки.Номинальная процентная ставка не отражает эффекты начисления сложных процентов или даже комиссий, связанных с этими финансовыми продуктами. Эффективная годовая процентная ставка — это реальный доход.

Ключевые выводы

Рекламируется сберегательный счет или ссуда как с номинальной процентной ставкой, так и с эффективной годовой процентной ставкой.
Эффективная годовая процентная ставка — это реальный доход, выплачиваемый на сбережения, или реальная стоимость ссуды, поскольку она учитывает эффекты начисления сложных процентов и любые взимаемые комиссии.
Чем чаще периоды начисления сложных процентов, тем выше доход.

Вот почему эффективная годовая процентная ставка — важная финансовая концепция, которую необходимо понять. Точно сравнивать различные предложения можно только в том случае, если вы знаете эффективные годовые процентные ставки по каждому из них.

Пример эффективной годовой процентной ставки

Например, рассмотрите эти два предложения: Инвестиция A платит 10% годовых, начисляемых ежемесячно. Инвестиции B выплачиваются 10,1% каждые полгода.Какое предложение лучше?

В обоих случаях рекламируемая процентная ставка является номинальной процентной ставкой. (количество периодов начисления сложных процентов) — 1

Для инвестиции A это будет: 10.2 — 1

Инвестиция B имеет более высокую заявленную номинальную процентную ставку, но эффективная годовая процентная ставка ниже, чем эффективная ставка для инвестиции A. Это связано с тем, что инвестиции B составляют меньше раз в течение года.

Если инвестор вложит, скажем, 5 000 000 долларов в одну из этих инвестиций, неправильное решение будет стоить более 5 800 долларов в год.

Более частое начисление сложных процентов дает более высокую прибыль

По мере увеличения количества периодов начисления сложных процентов увеличивается и эффективная годовая процентная ставка.Квартальное начисление сложных процентов дает более высокую доходность, чем полугодовое начисление сложных процентов, ежемесячное начисление сложных процентов больше, чем ежеквартально, а ежедневное начисление сложных процентов больше, чем ежемесячно. Ниже приводится разбивка результатов этих различных составных периодов с номинальной процентной ставкой 10%:

Полугодовой = 10,250%
Ежеквартально = 10,381%
Ежемесячно = 10,471%
Ежедневно = 10,516%

Пределы компаундирования

Есть потолок феномену компаундирования.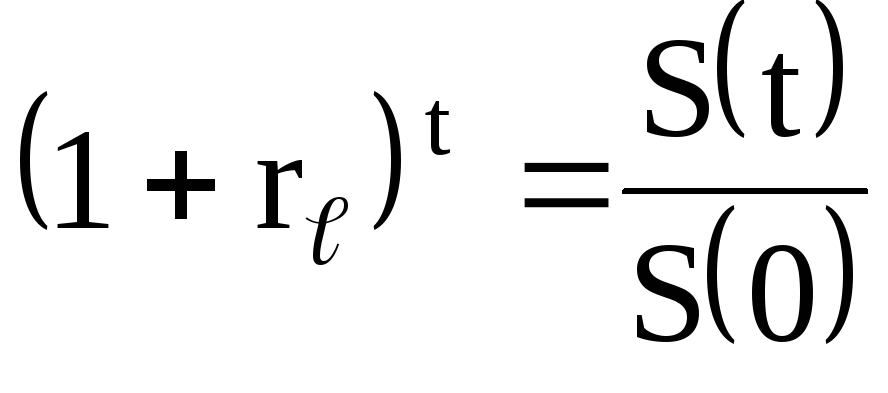 (0,1) — 1.

Часто задаваемые вопросы

Какова эффективная годовая процентная ставка?

Эффективная годовая процентная ставка — это важное понятие, которое описывает истинную процентную ставку, связанную с инвестированием или ссудой. Наиболее важной особенностью эффективной годовой процентной ставки является то, что она учитывает тот факт, что более частые периоды начисления сложных процентов приведут к более высокой эффективной процентной ставке. Например, предположим, что у вас есть две ссуды, каждая из которых имеет установленную процентную ставку 10%, в которой один составляет ежегодно, а другой — два раза в год.Несмотря на то, что у них обоих заявленная процентная ставка составляет 10%, эффективная годовая процентная ставка по ссуде, которая составляет два раза в год, будет выше.

Как рассчитать эффективную годовую процентную ставку?

Эффективная годовая процентная ставка рассчитывается по следующей формуле:

Взаимодействие с другими людьми

ты

знак равно

(

)

—

где:

знак равно

Номинальная процентная ставка

знак равно

Количество периодов

\ begin {align} & Effective \ Annual \ Interest \ Rate = \ left (1+ \ frac {i} {n} \ right) ^ n-1 \\ & \ textbf {где:} \\ & i = \ text {Номинальный процентная ставка} \\ & n = \ text {Количество периодов} \\ \ end {выровнено}
Эффективная годовая процентная ставка = (1 + ni) n − 1, где: i = номинальная процентная ставка = количество периодов

Хотя это можно сделать вручную, большинство инвесторов будут использовать финансовый калькулятор, электронную таблицу или онлайн-программу. Более того, инвестиционные веб-сайты и другие финансовые ресурсы регулярно публикуют эффективную годовую процентную ставку ссуды или инвестиции. Эта цифра также часто включается в проспект эмиссии и маркетинговые документы, подготовленные эмитентами ценных бумаг.

Почему важна эффективная годовая процентная ставка?

Эффективная годовая процентная ставка важна, потому что без нее заемщики могут быть введены в заблуждение и недооценивают истинную стоимость ссуды. Это, в свою очередь, может привести к финансовым проблемам, если заемщик не внесет в бюджет полную сумму своих процентных платежей.С другой стороны, для инвесторов расчет эффективной годовой процентной ставки важен для прогнозирования фактического ожидаемого дохода от инвестиций, таких как корпоративные облигации или другие ценные бумаги с фиксированным доходом. В противном случае они могут недооценить реальную привлекательность инвестиционной возможности.

Эффективная годовая ставка — определение, формула, что вам нужно знать

Что такое эффективная годовая ставка?

Эффективная годовая ставка (EAR) — это процентная ставка. Процентные расходы. Процентные расходы возникают из-за компании, которая финансируется за счет заемных средств или аренды капитала.Проценты указываются в отчете о прибылях и убытках, но также могут быть фактически заработаны от инвестиций или выплачены по ссуде в результате сложения процентов за определенный период времени. Обычно она выше номинальной ставки и используется для сравнения различных финансовых продуктов, которые рассчитывают годовой процент с разными периодами начисления сложных процентов — еженедельно, ежемесячно, ежегодно и т. Д. Увеличение количества периодов начисления сложных процентов приводит к увеличению эффективной годовой процентной ставки с течением времени .

Эффективная годовая ставка обычно выше номинальной, потому что номинальная ставка соответствует годовой процентной ставке независимо от начисления сложных процентов.Увеличение количества периодов начисления сложных процентов увеличивает эффективную годовую ставку по сравнению с номинальной. (количество периодов начисления сложных процентов) — 1

Например:

Union Банк предлагает г-ну господину номинальную процентную ставку 12% по своему депозитному сертификату.Обама, клиент банка. Первоначально клиент инвестировал 1000 долларов и согласился на ежемесячное начисление процентов в течение одного полного года. В результате начисления сложных процентов эффективная процентная ставка составляет 12,683%, при этом деньги выросли на 126,83 доллара за один год, хотя процентная ставка предлагается только на уровне 12%.

Калькулятор эффективной годовой ставки

Ниже приведен снимок экрана с бесплатным калькулятором эффективной годовой ставки (EAR) CFI.

Как видно из приведенного выше примера, номинальная процентная ставка равна 8.0% с 12 периодами начисления сложных процентов в год соответствует эффективной годовой процентной ставке (EAPR) 8,3%.

Скачать бесплатный шаблон

Введите свое имя и адрес электронной почты в форму ниже и загрузите бесплатный шаблон прямо сейчас!

Калькулятор эффективной годовой ставки

Загрузите бесплатный шаблон Excel, чтобы углубить свои знания в области финансов!

Что такое номинальная процентная ставка?

Номинальная процентная ставка — это заявленная ставка, указанная для финансового инструмента, выпущенного кредитором или поручителем. Эта ставка является основой для расчета суммы процентов в результате сложения основной суммы плюс проценты за период времени. По сути, это реальная денежная цена, которую заемщики платят кредиторам или которую инвесторы получают от эмитентов.

Что такое комплексный период?

Период начисления сложных процентов — это период времени, по истечении которого непогашенная ссуда или инвестиционные проценты добавляются к основной сумме указанной ссуды или инвестиции. Период может быть ежедневным, еженедельным, ежемесячным, ежеквартальным или полугодовым, в зависимости от условий, согласованных заинтересованными сторонами.По мере увеличения количества периодов начисления сложных процентов увеличивается и сумма процентов, заработанных или выплаченных на использованные деньги. Квартальное начисление сложных процентов дает более высокую доходность, чем полугодовое сложение, в то время как ежемесячное начисление сложных процентов приносит больше, чем ежеквартально, а ежедневное начисление сложных процентов приносит больше, чем ежемесячно.

Подробнее о процентных ставках

Чтобы узнать больше о процентных ставках, посетите бесплатные онлайн-курсы CFI по финансам и бухгалтерскому учету!

Насколько важна эффективная годовая ставка в бизнесе?

Эффективная годовая процентная ставка — полезный способ оценки фактической отдачи от инвестиций и определения процентных расходов, уплаченных по ссуде.Заемщики должны иметь твердое представление о влиянии стоимости долга Стоимость долга Стоимость долга — это доход, который компания предоставляет своим держателям долга и кредиторам. Стоимость долга используется в расчетах WACC для анализа оценки. влияет на их бизнес, так как это повлияет на их прибыльность и платежеспособность.

Более высокие процентные расходы снижают коэффициент покрытия процентов. Коэффициент покрытия Коэффициент покрытия используется для измерения способности компании выплачивать свои финансовые обязательства. Более высокий коэффициент указывает на большую способность компании выполнять обязательства, что может снизить ее способность обслуживать долг в будущем. Кроме того, более высокие процентные расходы снизят чистую прибыль и прибыльность компании (при прочих равных).

С другой стороны, инвесторы выиграют, если эффективная процентная ставка выше номинальной ставки, предлагаемой эмитентом. Они также используют эту ставку для сравнения различных инвестиционных портфелей, используя разные периоды начисления сложных процентов, чтобы принять эффективное решение.

Дополнительное обучение

CFI — глобальный провайдер Программы сертификации финансового моделирования. Станьте сертифицированным аналитиком финансового моделирования и оценки (FMVA) ®, разработанной, чтобы научить любого стать финансовым аналитиком мирового уровня.Если вы заинтересованы в продвижении своей карьеры в сфере корпоративных финансов, эти статьи CFI помогут вам на этом пути:

Средневзвешенная стоимость капитала (WACC) WACCWACC — это средневзвешенная стоимость капитала компании, которая представляет собой смешанную стоимость капитала. включая капитал и долг.
EBITDAEBITDAEBITDA или прибыль до вычета процентов, налогов, износа и амортизации — это прибыль компании до того, как будет произведен какой-либо из этих чистых вычетов. EBITDA фокусируется на операционных решениях бизнеса, потому что он смотрит на прибыльность бизнеса от основных операций до влияния структуры капитала.Формула, примеры
Базовые точки (bps) Базовые точки (BPS) Базовые точки (BPS) — это обычно используемая метрика для измерения изменений процентных ставок. Базовая точка — одна сотая процента.
XIRR против IRR XIRR против IRR Зачем использовать XIRR против IRR. XIRR назначает конкретные даты каждому отдельному денежному потоку, что делает его более точным, чем IRR, при построении финансовой модели в Excel.
Инвестиционный банкингИнвестиционный банкингИнвестиционный банкинг — это подразделение банка или финансового учреждения, которое обслуживает правительства, корпорации и учреждения, предоставляя консультационные услуги по андеррайтингу (привлечению капитала) и слияниям и поглощениям (M&A). Инвестиционные банки выступают в качестве посредников
Финансовое моделированиеЧто такое финансовое моделирование Финансовое моделирование выполняется в Excel для прогнозирования финансовых показателей компании. Обзор того, что такое финансовое моделирование, как и зачем его создавать.

Эффективная годовая ставка (EAR) — Как рассчитать эффективную процентную ставку

Что такое эффективная годовая процентная ставка?

Эффективная годовая процентная ставка (EAR) — это процентная ставка, скорректированная с учетом начисления сложных темпов роста Совокупный темп роста — это мера, используемая специально в контексте бизнеса и инвестирования, которая показывает скорость роста за несколько периодов времени.Это показатель постоянного роста ряда данных. Самым большим преимуществом совокупной скорости роста является то, что метрика учитывает эффект сложения. за определенный период. Проще говоря, эффективная годовая процентная ставка — это процентная ставка. Процентные расходы. Процентные расходы возникают из-за компании, которая финансирует за счет заемных средств или аренды капитала. Процентная ставка указывается в отчете о прибылях и убытках, но также может указываться, что инвестор может заработать (или заплатить) через год после учета сложного процента.

EAR можно использовать для оценки процентов, подлежащих уплате по ссуде или долгу, или для оценки доходов от инвестиций, таких как гарантированный инвестиционный сертификат (GIC) или сберегательный счет.

Эффективная годовая процентная ставка также известна как эффективная процентная ставка (EIR), годовая эквивалентная ставка (AER) или эффективная ставка. Сравните это с годовой процентной ставкой (APR). Годовая процентная ставка (APR) Годовая процентная ставка (APR) — это годовая процентная ставка, которую физическое лицо должно платить по ссуде или которую они получают на депозитный счет.В конечном счете, годовая процентная ставка — это простой процентный термин, используемый для выражения числовой суммы, ежегодно выплачиваемой физическим или юридическим лицом за право заимствования денег. который основан на простом интересеПростой интересПростой процентной формуле, определении и примере. Простой процент — это расчет процентов, который не учитывает эффект начисления процентов. Во многих случаях проценты складываются с каждым назначенным периодом ссуды, но в случае простых процентов это не так. Расчет простых процентов равен основной сумме, умноженной на процентную ставку, умноженной на количество периодов..

Формула EAR приведена ниже:

Где:

i = Заявленная годовая процентная ставка
n = Количество периодов начисления сложных процентов

Эффективная годовая ставка на основе начисления сложных процентов

В таблице ниже показана разница в эффективной годовой ставке при изменении периодов начисления сложных процентов.

Таблица: Курс CFI по основам фиксированного дохода

Например, EAR установленной процентной ставки 1%, начисляемой ежеквартально, равен 1. 0038%.

Важность эффективной годовой ставки

Эффективная годовая процентная ставка — важный инструмент, позволяющий оценить истинную доходность инвестиций или истинную процентную ставку по ссуде.

Заявленная годовая процентная ставка и эффективная процентная ставка могут значительно отличаться из-за начисления сложных процентов. Эффективная процентная ставка важна для определения наилучшего кредита или определения того, какие инвестиции предлагают наибольшую доходность.Внутренняя норма доходности (IRR) Внутренняя норма доходности (IRR) — это ставка дисконтирования, которая делает чистую приведенную стоимость (NPV) проекта равной нулю. Другими словами, это ожидаемая совокупная годовая норма прибыли, которая будет получена от проекта или инвестиций.

В случае начисления сложных процентов EAR всегда выше установленной годовой процентной ставки.

EAR Пример

Например, предположим, что банк предлагает вашему депозиту в размере 10 000 долларов США установленную процентную ставку 12%, начисляемую ежемесячно. В таблице ниже представлена концепция эффективной годовой процентной ставки:

Таблица: Курс CFI по основам фиксированного дохода

Процентная ставка за 1 месяц: начальный баланс (10 000 долларов) x процентная ставка (12% / 12 = 1% ) = 100 долларов США

Процентная ставка за месяц 2: Начальный баланс (10 100 долларов США) x процентная ставка (12% / 12 = 1%) = 101 доллар США

Изменение в процентах от начального баланса (10000 долларов США) до конечного баланса ( 11 268 долларов США) равно (11 268 долларов США — 10 000 долларов США) / 10 000 долларов США =.12683 или 12,683%, что является эффективной годовой процентной ставкой. Несмотря на то, что банк предложил заявленную процентную ставку 12%, ваши деньги выросли на 12,683% за счет ежемесячного начисления сложных процентов.

Эффективная годовая процентная ставка позволяет определить истинную рентабельность инвестиций (ROI) Формула ROI (Return on Investment) Рентабельность инвестиций (ROI) — это финансовый коэффициент, используемый для расчета выгоды, которую инвестор получит по отношению к своим инвестициям. Стоимость. Чаще всего он измеряется как чистая прибыль, деленная на первоначальные капитальные затраты на инвестиции.Чем выше коэффициент, тем больше полученная выгода.

Скачать бесплатный шаблон

Введите свое имя и адрес электронной почты в форму ниже и загрузите бесплатный шаблон, показанный выше прямо сейчас!

Калькулятор эффективной годовой процентной ставки

Загрузите бесплатный шаблон Excel, чтобы углубить свои знания в области финансов!

Как рассчитать эффективную процентную ставку?

Чтобы рассчитать эффективную процентную ставку по формуле EAR, выполните следующие действия:

1.Определите заявленную процентную ставку

Заявленную процентную ставку (также называемую годовой процентной ставкой или номинальной ставкой) обычно можно найти в заголовках кредитного или депозитного договора. Пример: «Годовая ставка 36%, проценты взимаются ежемесячно».

2. Определите количество периодов начисления сложных процентов

Периоды начисления сложных процентов обычно бывают ежемесячными или ежеквартальными. Периоды начисления сложных процентов могут составлять 12 (12 месяцев в году) и 4 квартальных (4 квартала в году).

Для справки:

Ежемесячно = 12 периодов начисления начислений
Квартально = 4 периода начисления начислений
Двухнедельные = 26 периодов начисления начислений
Еженедельно = 52 периода начисления начислений
Ежедневно = 365 периодов начисления начислений

3 .Примените формулу EAR: EAR = (1+ i / n)

ⁿ — 1

Где:

- i = заявленная процентная ставка
- n = периоды начисления процентов

Пример

Для расчета эффективной годовой процентной ставки по кредитной карте с годовой ставкой 36% и ежемесячным начислением процентов:

1. Заявленная процентная ставка: 36%

2. Количество периодов начисления сложных процентов: 12

Таким образом, EAR = (1 + 0. 12 — 1 = 0,4257 или 42,57%.

Почему банки не используют эффективную годовую процентную ставку?

Когда банки взимают проценты, вместо эффективной годовой процентной ставки используется указанная процентная ставка. Это делается для того, чтобы потребители поверили, что они платят более низкую процентную ставку.

Например, для ссуды с установленной процентной ставкой 30%, начисляемой ежемесячно, эффективная годовая процентная ставка будет 34,48%. Банки обычно рекламируют заявленную процентную ставку 30%, а не эффективную процентную ставку 34.48%.

Когда банки выплачивают проценты по вашему депозитному счету, EAR объявляется более привлекательным, чем заявленная процентная ставка.

Например, для депозита с установленной ставкой 10% ежемесячно, эффективная годовая процентная ставка будет 10,47%. Банки будут рекламировать эффективную годовую процентную ставку 10,47%, а не заявленную процентную ставку в 10%.

По сути, они показывают ту ставку, которая кажется более благоприятной.

Дополнительная литература

CFI — глобальный поставщик курсов финансового моделирования и сертификации финансовых аналитиков. Станьте сертифицированным аналитиком финансового моделирования и оценки (FMVA) ®.Чтобы продолжить карьеру финансового профессионала, ознакомьтесь со следующими дополнительными ресурсами CFI:

Ожидаемая доходность Ожидаемая доходность Ожидаемая доходность инвестиций — это ожидаемая величина распределения вероятностей возможной прибыли, которую они могут предоставить инвесторам. Возврат инвестиций — это неизвестная переменная, которая имеет разные значения, связанные с разными вероятностями.
Базисные баллы Базисные баллы (BPS) Базовые баллы (BPS) — это обычно используемая метрика для измерения изменений процентных ставок.Базовая точка — одна сотая процента.
Прирост капитала YieldCapital Gains Доходность Доходность прироста капитала (CGY) — это увеличение цены инвестиции или ценной бумаги, выраженное в процентах. Поскольку расчет доходности прироста капитала включает рыночную цену ценной бумаги с течением времени, его можно использовать для анализа колебаний рыночной цены ценной бумаги. См. Расчет и пример
Средневзвешенная стоимость капитала (WACC) WACCWACC — это средневзвешенная стоимость капитала фирмы, которая представляет собой смешанную стоимость капитала, включая собственный капитал и заемные средства.

Как рассчитать эффективную процентную ставку — AccountingTools

Эффективная процентная ставка — это ставка использования, которую заемщик фактически платит по ссуде. Это также может рассматриваться как рыночная процентная ставка или доходность к погашению. Эта ставка может отличаться от ставки, указанной в кредитном документе, на основании анализа нескольких факторов; более высокая эффективная ставка может побудить заемщика обратиться к другому кредитору. Это следующие факторы:

Количество начислений долга в течение года
Фактическая сумма выплаченных процентов
Сумма, уплаченная инвестором за долг

При учете только влияния При начислении сложных процентов на процентную ставку шаги, необходимые для расчета эффективной процентной ставки, следующие:

Найдите в ссудных документах период начисления сложных процентов. 4-1 = 10,38% Эффективная процентная ставка
Существуют и другие обстоятельства, которые могут изменить выплачиваемую процентную ставку в еще большей степени. Примите во внимание следующие дополнительные факторы:
- Дополнительные сборы . Заемщик может платить дополнительные сборы, которые представляют собой скрытую форму процентных расходов. Эти сборы стоит включить в расчет, если они существенны.
- Измененная сумма ссуды . Если инвестор не согласен с тем, что рыночная процентная ставка соответствует заявленной процентной ставке, подлежащей выплате заемщиком, инвестор может предложить цену, меньшую или большую, чем номинальная сумма, для приобретения долга.Таким образом, если рыночная процентная ставка выше номинальной суммы долгового инструмента, заемщик платит меньше по долгу, тем самым создавая более высокую эффективную доходность. И наоборот, если рыночная процентная ставка ниже номинальной суммы долгового инструмента, заемщик готов заплатить больше по долгу.
Проведение полного анализа эффективной процентной ставки может оказаться весьма полезным для заемщика, который может обнаружить, что следует избегать соглашения о предполагаемом заимствовании.Эта концепция также полезна для сравнения нескольких альтернативных механизмов кредитования или заимствования, которые включают различные расчеты процентных ставок.
Связанные курсы
Формулы и функции Excel
Финансовый анализ
Введение в Excel
Как рассчитать эффективную годовую процентную ставку
Интересующие вопросы могут не быть интересными для многих. Многие люди паникуют, когда дело доходит до сложного финансового жаргона и сокращений. Тем не менее, если вы занимаетесь предоставлением кредитов, важно понимать, как рассчитываются процентные ставки.В самом деле, если вы ведете бизнес, в котором используются кредиты (что вы почти наверняка делаете), это также важно понимать. Здесь мы рассмотрим, как рассчитать эффективную годовую процентную ставку (EAR), чтобы вы могли лучше понять проценты, подлежащие выплате (или полученные) по кредиту, который вы предлагаете и используете.
Что такое эффективная годовая процентная ставка?
Чтобы лучше понять реальное влияние процентов на наш бизнес, нам необходимо принимать во внимание комплексные проценты.Всякий раз, когда рекламируются процентные ставки (номинальные ставки), начисление сложных процентов не учитывается. Но если мы не сделаем это сами, у нас могут остаться неточные прогнозы денежных потоков и вероятность пропущенных или просроченных платежей, которые могут повлечь за собой дополнительные расходы и еще больше поставить под угрозу нашу ликвидность.
Проще говоря, EAR — это проценты, которые выплачиваются в реальном выражении по любой ссуде, кредитной карте или другому долгу, который вы предоставляете или используете. Это то, что вы используете для расчета своих доходов по кредиту, который вы предоставляете своим клиентам, или ваших реальных обязательств перед кредиторами.
Понимание формулы EAR
Хотя существует полезный калькулятор эффективной годовой процентной ставки, который может автоматизировать этот процесс, важно знать формулу самостоятельно. Это требует от вас понимания двух переменных. Объявленная номинальная годовая процентная ставка (которую мы будем называть r) и количество периодов, в течение которых начисляются проценты (i). Поскольку обычно это месяцы, мы будем обозначать это как m.
Таким образом, формула для расчета EAR (которую мы будем называть i) выглядит так:
i = (1 + r / m) xm −1
Чем больше периодов начисления сложных процентов у вас есть, тем больше вы можете ожидать, что ваш EAR увеличится.Таким образом, квартальное начисление сложных процентов дает более высокую прибыль, чем начисление сложных процентов каждые шесть месяцев, в то время как ежемесячное начисление сложных процентов дает больше, чем квартальное. Некоторые кредиторы даже ежедневно прибавляют.
Конечно, если вы не слишком разбираетесь в математике, эту формулу может быть сложно контекстуализировать. Итак, давайте рассмотрим наглядный пример.
Пример эффективной годовой процентной ставки
Допустим, вам необходимо новое оборудование для вашей компании. Вы знаете, что это оборудование будет стоить вам 5000 долларов, но у вас недостаточно ликвидности, чтобы покрыть эту стоимость, не нарушив ваш денежный поток.(количество периодов начисления сложных процентов) — 1
Для банка A это будет: 10,47% = (1 + (10% / 12)) x 12 — 1
Для банка B это будет: 10,36 % = (1 + (10,1% / 2)) x 2 — 1

Итак, хотя у банка B может быть немного более высокая номинальная процентная ставка, у него более низкий EAR, чем у банка A, потому что он составляет меньше раз в течение курса года. Хотя эта разница может привести только к экономии 5,80 долларов в год для ссуды в 5000 долларов, если вам нужно было занять значительно больше, разница может действительно возрасти!

Мы можем помочь

Если вы хотите узнать больше о расчете эффективной годовой процентной ставки, свяжитесь с финансовыми экспертами GoCardless.Узнайте, как GoCardless может помочь вам со специальными или регулярными платежами.

GoCardless используется более чем 55 000 компаний по всему миру. Узнайте больше о том, как вы можете улучшить обработку платежей в своем бизнесе уже сегодня.

Узнать больше Зарегистрироваться

Номинальная, периодическая и эффективная процентная ставка

Номинальная, периодическая и эффективная процентная ставка на основе дискретного сложения процентов

Обычно финансовые агентства сообщают процентную ставку на номинальной годовой основе с указанным периодом начисления сложных процентов, который показывает, сколько раз начисляются проценты в год.Это называется простой процентной ставкой, номинальной процентной ставкой или годовой процентной ставкой. Если процентная ставка начисляется ежегодно, это означает, что проценты начисляются один раз в год, и вы получаете проценты в конце года. Например, если вы поместите 100 долларов на банковский счет с годовой процентной ставкой 6% годовых, вы получите 100 * (1 + 0,06) = 106 долларов в конце года.

Но период начисления сложных процентов может быть меньше года (он может быть квартальным, ежемесячным или ежедневным). В этом случае процентная ставка будет увеличиваться более одного раза в год. Например, если финансовое агентство отчитывается о квартальном начислении сложных процентов, это означает, что проценты будут начисляться четыре раза в год, и вы будете получать проценты в конце каждого квартала. Если проценты начисляются ежемесячно, тогда проценты начисляются 12 раз в год, и вы получите проценты в конце месяца.

Например: предположим, что вы кладете 100 долларов на банковский счет, и банк ежемесячно выплачивает вам 6% годовых.Это означает, что номинальная годовая процентная ставка составляет 6%, проценты начисляются каждый месяц (12 раз в год) со ставкой 6/12 = 0,005 в месяц, и вы получаете проценты в конце каждого месяца. В этом случае в конце года вы получите 100 * (1 + 0,005) 12 = 106,17 долларов, что больше, чем при начислении раз в год: 100 * (1 + 0,06) 1 = 106 долларов. Следовательно, чем больше периодов начисления сложных процентов в году, тем больше общая сумма выплачиваемых процентов.

Посмотрите следующее видео: Номинальные и периодические процентные ставки (время 3:52).

Номинальные и периодические процентные ставки

Щелкните, чтобы просмотреть стенограмму видеоролика «Номинальные и периодические процентные ставки».

ВЕДУЩИЙ

: В этом видео я собираюсь объяснить номинальные, периодические и эффективные процентные ставки. Финансовые агентства обычно сообщают процентную ставку ежегодно. Процентная ставка может увеличиваться один или несколько раз в год. Если процентная ставка начисляется ежегодно, это означает, что процентная ставка начисляется один раз в год.Если процентная ставка начисляется ежеквартально, то процентная ставка увеличивается четыре раза в год. И если процентная ставка начисляется ежемесячно, это означает, что процентная ставка увеличивается 12 раз в год.

Давайте поработаем на примере. Предположим, вы вкладываете 100 долларов на воображаемый банковский счет, который дает вам 6% годовых, начисляемых ежегодно. Таким образом, номинальная процентная ставка составляет 6% годовых. Процентная ставка в размере 6% начисляется один раз в год, и вы получите проценты и основную сумму своих денег в конце первого года.Таким образом, вы получите 100 долларов, умноженные на 1, плюс 6% в степени 1 в конце первого года, что равняется 106 долларам.

Теперь предположим, что банк выплачивает вам 6% годовых, начисляемых ежеквартально. Таким образом, это означает, что номинальная процентная ставка составляет 6% в квартал, или процентная ставка будет увеличиваться четыре раза в год, а процентная ставка рассчитывается в конце каждого квартала. Чтобы рассчитать сумму денег, которую вы получите в конце первого года, нам нужно рассчитать процентную ставку за период, которая будет составлять 6%, разделенные на 4, и она равна 1.5%. Вы вносите свои 100 долларов в настоящее время, и банк начисляет проценты по ставке 1,5% за квартал. В году четыре квартала, поэтому проценты будут начисляться четыре раза в год по ставке 1,5% за квартал. Затем, в конце года, вы получите 100 долларов, умноженные на 1 плюс 0,15 в степени 4, что равняется 106 долларам плюс 0,14 доллара. Как видите, если банк учитывает процентную ставку, которая начисляется ежеквартально, он даст вам немного более высокий процент по сравнению со случаем, когда процентная ставка начисляется ежегодно.

Теперь предположим, что банк выплачивает вам 6% начисленных процентов ежемесячно, что означает, что процентная ставка начисляется 12 раз в год. В этом случае банк начисляет проценты каждый месяц. Как и в предыдущем примере, процентная ставка за период будет равна 6%, разделенным на 12, что составит 0,5% в месяц. И вы получите 100 долларов, умноженные на 1 плюс 0,005 в степени 12, что равняется 106 долларам плюс 0,17 доллара. Потому что существует 12 периодов начисления сложных процентов, а процентная ставка за период 0,5%. Как видите, процентная ставка начисляется ежемесячно, поэтому в конце года вы получите немного больше денег.Чем больше у вас начислений сложных процентов в год, тем выше будут проценты в конце года.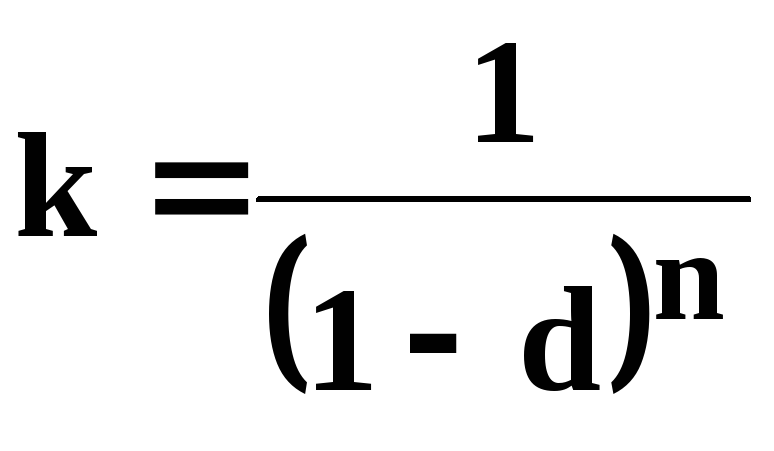

Кредит: Фарид Тайари

Процентная ставка за период i = r / m
Где m = количество периодов начисления сложных процентов в год
r = номинальная процентная ставка = миль

« Эффективная процентная ставка — это процентная ставка, которая при применении один раз в год к основной сумме дает такую же сумму процентов, равную номинальной ставке r процентов в год, начисляемой m раз в год.Годовая процентная доходность (APY) — это стандартный термин, используемый в банковской сфере для определения эффективной процентной ставки. «

Будущая стоимость, F1 , инвестирования P при i % за период на м за период после одного года:

P	_	_	_	_	_	F1 = P (F / P _{i, m}) = P (1 + i) ^m

	0	1	2	. ..	м период в год

И если эффективная процентная ставка E, применяется один раз в год, то будущая стоимость, F2 , инвестирования P по E% в год:

п.	_	_	F2 = P (F / P _{E, 1}) = P (1 + E) ¹

	0	1 период в год

Тогда:

F1 = F2P (1 + i) m = P (1 + E) 1

Так как P одинаково с обеих сторон: (1 + i) m = E + 1

Тогда:

Эффективная годовая процентная ставка: E = (1 + i) m − 1

(Уравнение 2-1)

Если эффективная годовая процентная ставка, E , известна, а процентная ставка за эквивалентный период i неизвестна, уравнение 2-1 может быть записано как:

я = (E +1) 1 / м −1

(Уравнение 2-2)

Возвращаясь к предыдущему примеру, i = 6/12 = 0. 005so, E = (1 + 0,005) 12−1 = 1,0617 — 1 = 0,0617 или 6,17%

Посмотрите следующее видео , Эффективная процентная ставка (время 4:02).

Эффективная процентная ставка

Щелкните, чтобы увидеть стенограмму видео «Эффективная процентная ставка».

ВЕДУЩИЙ: В этом видео я собираюсь объяснить, как рассчитать эффективную процентную ставку. В предыдущем видео мы узнали, как рассчитать процентную ставку за период, которая представляет собой номинальную процентную ставку r, деленную на количество периодов начисления сложных процентов в год, m.Таким образом, чтобы рассчитать будущую стоимость, вам нужно знать количество периодов от настоящего времени и желаемого будущего, а также процентную ставку за период. Например, f, будущее значение на конец первого года равно p, умножьте 1 на i, степень m, где m — количество периодов начисления сложных процентов в год.

Эффективная процентная ставка — это процентная ставка, которая при применении один раз в год дает вам такую же сумму процентов, равную номинальной ставке r. Годовая процентная доходность или APY — это термин, который используется в банковской сфере для обозначения эффективной процентной ставки.Вы можете увидеть здесь, когда где-то читаете, что, например, процентная ставка составляет 6% ежемесячно, это немного сбивает с толку. Потому что он не сообщает вам, какой будет фактическая годовая процентная ставка. Эффективная процентная ставка — это ставка, которая нам здесь помогает. Эффективная процентная ставка — это годовая ставка, которая дает вам точно такой же процент, равный номинальной ставке, которая начисляется несколько раз в год.

Возвращаясь к примеру в предыдущем видео, вы видели, что если вы поместите 100 долларов на банковский счет, который дает вам 6% -ную ежемесячную процентную ставку, вы получите 106 долларов плюс 0 долларов.17 в год. Таким образом, вы можете предположить, что эффективная процентная ставка здесь может составлять 6,17%. Теперь посмотрим, сможем ли мы найти общее уравнение. На предыдущем слайде я объяснил, как мы рассчитываем будущее значение F1 в конце первого года на основе процентной ставки периода i и количества периодов начисления сложных процентов в году m.

Если вы хотите рассчитать будущую стоимость в конце первого года, используя эффективную процентную ставку, здесь мы показываем это, мы должны иметь F2 равным P, умножить 1 плюс E степень 1. Эффективная процентная ставка равна E И мы хотим, чтобы рассчитать будущую стоимость в конце первого года.Будущая стоимость денег в конце первого года с использованием процентной ставки за период и эффективной процентной ставки должна быть равна. Значит, F1 должен быть равен F2.

И у нас есть уравнение 2-1. Это уравнение можно записать для i. E — эффективная процентная ставка. m — количество периодов начисления сложных процентов в году, а i — процентная ставка за период. Возвращаясь к примеру в предыдущем видео, мы положили 800 долларов на банковский счет, который дает нам 6% начисленных процентов ежемесячно. Чтобы рассчитать эффективную процентную ставку, нам нужно сначала рассчитать процентную ставку за период, а затем использовать уравнение, которое мы только что извлекли.Таким образом, эффективная процентная ставка будет 6,17%, что означает, что если мы применим процентную ставку 6,17% в год, это даст нам точно такую же будущую ценность, как и применение процентной ставки в размере 6%, начисленной ежемесячно.

Кредит: Фарид Тайари

, пример 2-1:

Предположим, что инвестиция приносит вам 2000 долларов в конце первого, второго и третьего года с годовой процентной ставкой 12%, начисляемой ежеквартально. Рассчитайте приведенную стоимость в нулевой момент времени и будущую стоимость этих платежей через три года.


P =?	_	_	_	_	2000	_	_	_	2000	_	_	_	2000	F =?

	0	1	2	3	4	5	6	7	8	9	10	11	12

Квартальная процентная ставка i = 12/4 = 3%

P = 2,000 * (P / F3%, 4) + 2,000 * (P / F3%, 8) + 2,000 * (P / F3%, 12) = 2000 [1 / (1 + 0. 03) 4] +2000 [(1 + 1 / 0,03) 8] +2000 [1 / (1 + 0,03) 12] = 4 758,55 долл. США
F = 2 000 * (F / P3%, (12−4)) + 2 000 * (F / P3%, (12-8)) + 2,000 * (F / P3%, (12-12)) = 2,000 * (F / P3%, 8) + 2000 * (F / P3%, 4) + 2000 = 2000 * (1 + 0,03) 8 + 2000 * (1 + 0,03) 4+ 2000 = 6 784,56 долларов США

Обратите внимание, , что, поскольку процентная ставка начисляется ежеквартально, мы должны строить расчеты на квартальной основе. Таким образом, на временной шкале будет 12 кварталов (три года и 4 квартала в год).
Проценты в размере 2000 долларов выплачиваются в конце первого, второго и третьего года, которые будут последними кварталами каждого года (4 ^{-й квартал}, 8 ^{-й квартал} и 12 ^{-й квартал}). ).

Посмотрите следующее видео: Пример номинальной и периодической процентной ставки (время 3:45).

Номинальные и периодические процентные ставки

Щелкните, чтобы просмотреть стенограмму видеоролика «Пример номинальных и периодических процентных ставок».

ВЕДУЩИЙ: Давайте поработаем на примере. Предположим, есть инвестиция, которая приносит вам 2000 долларов в конце первого, второго и третьего года при годовой процентной ставке 12%, начисляемой ежеквартально.И мы хотим рассчитать текущую стоимость в нулевой момент времени и будущую стоимость в конце третьего года этих платежей.

Первое, что нам нужно сделать, это нарисовать временную шкалу и найти платежи на ней. Наименьший интервал на временной шкале должен быть периодом начисления сложных процентов, который в данном примере равен кварталу. Срок эксплуатации проекта — три года. Итак, у нас должно быть 12 кварталов или временной интервал на временной шкале.

Затем размещаем выплаты. Первый платеж в конце года, то есть в 4 квартале.Второй платеж в размере 2000 долларов будет произведен в конце второго года, то есть в 8-м квартале. И третий платеж в конце третьего года, то есть в двенадцатом квартале.

Теперь нам нужно рассчитать приведенную стоимость этих платежей. Но сначала нам нужно рассчитать процентную ставку за период, которая будет равна 12, разделенному на 4, и будет равно 3, потому что в году у нас 4 квартала. Очень важно отметить, что мы должны использовать процентную ставку периода, потому что наши временные интервалы являются квартальными.

Затем мы рассчитываем текущую стоимость этих платежей. Первый платеж производится в конце первого года, то есть в 4-м квартале, с процентной ставкой 3% за квартал. Второй платеж в 8 квартале с процентной ставкой 3% в квартал. И третьи 2000 долларов приходятся на 12 квартал с процентной ставкой 3%. И результат, который показывает текущую стоимость этих трех платежей.

Теперь, будущая стоимость. Опять же, сначала мы должны рассчитать процентную ставку за период, и она будет 3%.Затем мы рассчитываем будущую стоимость этих трех платежей. Под будущей стоимостью мы подразумеваем конец жизненного цикла проекта, то есть конец третьего года или 12-го квартала. Чтобы рассчитать текущую стоимость первого платежа, нам нужно знать, сколько периодов времени проходит между этим временем и будущим временем.

Первые 2000 долларов выплачиваются в 4-м квартале, что на 8 кварталов от будущего времени, потому что будущее время приходится на 12-й период. Таким образом, нам нужно записать 12 минус 4 как период времени здесь в множителе, потому что будущее время находится в 12-м периоде.Вторые 2000 долларов выплачиваются в конце второго года или 8-го квартала, что на 4 квартала от будущего времени. И последние 2000 долларов выплачиваются в конце третьего года или 12-го периода. Это то же время, что и мы желаем в будущем. И N или разница во времени будет равна нулю.

Кредит: Фарид Тайари

Непрерывное начисление процентов

Если годовая процентная ставка составляет ежегодно, то она должна увеличиваться один раз в год.
Если годовая процентная ставка составляет полугодие, то она должна увеличиваться дважды в год.
Если годовая процентная ставка составляет квартал, то она должна увеличиваться 4 раза в год.
Если годовая процентная ставка составляет ежемесячно, то она должна увеличиваться 12 раз в год.
Если годовая процентная ставка усугубляется ежедневно, то она должна увеличиваться 365 раз в год.
И если период начисления становится меньше, то количество начислений в год, м , становится больше. В пределе, когда м уходит в бесконечность, процент периода i приближается к нулю.Этот случай называется «Продолжает усугубление интереса». Используя дифференциальное исчисление, коэффициент суммы сложного платежа для непрерывного процентного платежа ( F / P _{r, n} ) можно рассчитать как:

F / Pr, n = ern

(Уравнение 2-3)

И, коэффициент текущей стоимости однократного дискретного платежа по продолжению начисления процентов ( P / Fr, n )

P / Fr, n = 1 / ern

(Уравнение 2-4)

r — номинальная процентная ставка, непрерывно начисляемая
n — количество периодов дискретной оценки
e — основание натурального логарифма (ln) = 2. 7183

, пример 2-2:

Давайте пересчитаем пример 2-1 с учетом продолжающейся сложной процентной ставки 12%:

P = 2,000 * (P / F12%, 1) + 2,000 * (P / F12%, 2) + 2,000 * (P / F12%, 3) = 2000 [1 / e0,12 * 1] +2000 [1 / e0,12 * 2] +2000 [1 / e0,12 * 3] = 4742,45 долл. СШАF = 2,000 * (F / P12%, 2) + 2,000 * (F / P12%, 1) + 2,000 = 2000 * e0,12 * 2 + 2000 * e0,12 * 1 + 2000 = 6 797,49 долл. США

Примечание: Следующие ссылки объясняют, как использовать функцию Excel (EXP) для вычисления e в степени числа:

Ссылка 1: Функция EXP в Excel
Ссылка 2: Функции Excel

Пожалуйста, посмотрите следующее видео, Непрерывное сложение процентов (время 4:54).

Непрерывное начисление процентов

Щелкните, чтобы увидеть стенограмму видео «Непрерывное усугубление интереса».

В этом видео я собираюсь объяснить непрерывное начисление сложных процентов и покажу вам, как рассчитать будущую и текущую стоимость в случае непрерывного начисления процентов.

Если у нас в году все больше и больше периода начисления сложных процентов, то период начисления процентов становится все меньше и меньше. Тогда количество периодов начисления сложных процентов в году m становится все больше и больше.Таким образом, в этом случае будущая стоимость может быть рассчитана как настоящее время: умножьте 1 плюс i, степень n, умножьте m. M — количество периодов начисления сложных процентов в год. I — периодическая процентная ставка, равная r, деленному на m, а r — номинальная процентная ставка, которая равна m, умноженному на i.

В пределе, когда m стремится к бесконечности, периодическая процентная ставка i, которая равна r, деленному на m, приближается к 0. В этом случае это называется непрерывным начислением процентов.

Теперь давайте вычислим коэффициент сложного количества, F над P, или коэффициент будущей стоимости для непрерывных процентов.Таким образом, этот множитель равен 1 плюс i в степени n, умноженной на m, и мы можем записать i как r вместо m.

Теперь нам нужно вычислить предел, когда m стремится к бесконечности. В этом случае этот член приближается к 0, а этот член стремится к бесконечности. Таким образом, мы можем извлечь здесь член e и вычислить предел как e power rn.

Таким образом, коэффициент сложного количества или коэффициент будущей стоимости для непрерывных процентов будет равен e power rn, или будущая стоимость может быть рассчитана как P умножить на e power rn. F — будущая стоимость непрерывного начисления сложных процентов.R — номинальная процентная ставка, начисляемая непрерывно, n — количество дискретных периодов оценки, которые могут составлять один год, два года, три года и т. Д. А е — основа натурального бревна.

Аналогичным образом мы можем рассчитать текущую стоимость в случае непрерывного начисления сложных процентов. Коэффициент текущей стоимости равен коэффициенту, обратному коэффициенту будущей стоимости. Таким образом, приведенная стоимость может быть рассчитана как P равно F, деленному на e степень r, n. P — это текущая стоимость непрерывного начисления сложных процентов.

А теперь поработаем на примере.Это предыдущий пример, но мы собираемся рассмотреть процентную ставку непрерывного начисления сложных процентов. Предположим, есть инвестиция, которая приносит вам 2000 долларов в конце первого, второго и третьего года, и вы хотите рассчитать приведенную стоимость в настоящее время и будущую стоимость в конце третьего года. И мы должны учитывать постоянную процентную ставку начисления сложных процентов в размере 12%.

Сначала мы рисуем временную шкалу. У нас будет три платежа по 2000 долларов в конце первого, второго и третьего года, и мы хотим рассчитать приведенную стоимость этих трех платежей.

Первый платеж будет в конце первого года. Таким образом, нам нужно дисконтировать это за один год с 12% непрерывной процентной ставки. Второй платеж будет в конце второго года, так что n будет 2. И последний платеж будет в третьем году, так что n равно 3.

А теперь подставляем множитель, который будет равен 1 на степень 12%, умноженную на 1 и так далее, и результат.

Теперь мы собираемся рассчитать будущую стоимость этих трех платежей.Первый платеж происходит в конце первого года, то есть через два года от будущего времени. Таким образом, n равно 2. Второй платеж находится на расстоянии одного года от будущего времени, поэтому n равно 1. И последний платеж происходит точно в то же время, что и будущее время, поэтому n равно 0, и мы записываем 2000 долларов, а не Не нужно никакого компаундирования. А затем заменяем факторы. E мощность 12% умножьте на 2 для первого платежа и так далее. И у нас есть результат.

Кредит: Фарид Тайари

«Фиксированная» или «Дополнительная» процентная ставка

Фиксированная или дополнительная процентная ставка применяется к основной сумме первоначальных инвестиций в каждый период начисления процентов .Это означает, что общий процент, полученный за инвестиции по фиксированной процентной ставке, рассчитывается линейно и представляет собой просто сумму процентов за все периоды. Например, если вы инвестируете 1000 долларов в настоящее время в проект с фиксированной процентной ставкой 12% годовых на 100 дней, то через 100 дней вы получите 32,88 доллара:
1000 * 0,12 * (100/365) = 32,88 доллара. Проценты
Фиксированная процентная ставка обычно применяется, когда проценты начисляются за часть года или периода.

Примечание. В инженерной экономике термин «простой процент» обычно используется как «дополнительная» или «фиксированная» процентная ставка, как определено здесь.

9.6: Эквивалентные и эффективные процентные ставки

Как можно сравнить процентные ставки, объявленные с различными сложными процентами? Например, предположим, что вы подумываете о покупке нового дома, поэтому последние несколько недель вы пытались найти финансирование. Вы разговаривали со многими банками, а также с местными ипотечными брокерами в выставочных домах. При полугодовом начислении сложных процентов самая низкая ставка, с которой вы столкнулись, составляет 6,6%. Посетив другой выставочный дом, вы встретите ипотечного брокера, предлагающего ипотеку на 6.57%. Мелким шрифтом это означает, что ставка начисляется ежеквартально. Вы помните из своего урока бизнес-математики, что начисление сложных процентов является важным компонентом процентной ставки, и задаетесь вопросом, какой из них вам следует выбрать — 6,6% в полугодовом выражении или 6,57% в квартальном исчислении.

При рассмотрении процентных ставок по ссудам вам явно нужна лучшая ставка. Если все ваши возможные ссуды составлены одинаково, выбор лучшей процентной ставки зависит от выбора наименьшего числа.Однако, когда процентные ставки складываются по-разному, наименьшее число на самом деле может быть не лучшим выбором. С другой стороны, в случае инвестиций вы хотите получать наибольшие проценты. Однако самая высокая номинальная ставка может быть не такой хорошей, как кажется, в зависимости от начисления сложных процентов.

Чтобы справедливо сравнить процентные ставки и выбрать лучшую, все они должны быть выражены с равным начислением сложных процентов. В этом разделе объясняется концепция эффективной процентной ставки, и вы научитесь преобразовывать процентные ставки с одной частоты начисления сложных процентов на другую частоту.

Эффективные процентные ставки

Если вы вложите 1000 долларов в инвестицию, приносящую 10% совокупный доход каждые полгода, сколько у вас будет на вашем счету через год? Менее 1100 долларов, ровно 1100 или больше 1100 долларов? Если вы говорите, что больше 1100 долларов, вы абсолютно правы. Другими словами, номинальная ставка 10% не полностью отражает истинную сумму процентов, которую инвестиции приносят ежегодно, которая зависит от того, как часто увеличивается основная сумма. Это вызывает два вопроса:

Какая точная сумма процентов зарабатывается ежегодно?
Какая годовая процентная ставка действительно зарабатывается?

Эффективная процентная ставка — это истинная годовая процентная ставка, которая эквивалентна процентной ставке, начисляемой с некоторой другой (не годовой) периодичностью.Другими словами, сумма процентов, начисленных по эффективной процентной ставке один раз в год, в точности равна сумме процентов, начисленных по периодической процентной ставке, последовательно начисляемой указанное количество раз в году. Чтобы рассчитать эффективную процентную ставку, вы должны преобразовать сложную процентную ставку от номинальной процентной ставки в годовое сложение.

Формула

Чтобы увидеть, как будет развиваться формула, возьмите инвестицию в размере 1000 долларов США с 10% -ным усложнением каждые полгода в течение всего года.{1} = \ 1 102,50 $ \ nonumber \]

Этот вариант дает ту же сумму процентов — 102,50 доллара. Другими словами, 10,25% в год дает тот же результат, что и 10%, получаемые раз в полгода. Следовательно, эффективная процентная ставка по вложениям составляет 10,25%, и это то, что инвестиции действительно приносят ежегодно.

Обобщая пример, вы рассчитываете будущую стоимость и сумму процентов для ставки 10%, начисляемых раз в полгода, по формулам

\ [FV = PV (1 + i) (1 + i) \ quad \ text {и} \ quad I = FV-PV \ nonumber \]

Обратите внимание, что периодические проценты увеличиваются с коэффициентом \ ((1 + i) \), количество раз равное частоте начисления сложных процентов (\ (CY = 2 \)).{CY} -1 \ nonumber \]

Формула 9.4 выражает это уравнение через переменные стоимости денег во времени. Кроме того, он адаптируется к любому преобразованию между различными частотами сложения.

Формула 9,4

Как это работает

Чтобы рассчитать эффективную процентную ставку, выполните следующие действия:

Шаг 1 : Определите известные переменные, включая исходную номинальную процентную ставку (\ (IY \)) и исходную частоту начисления сложных процентов (\ (CY_ {Old} = 1 \)).Установите \ (CY_ {New} = 1 \).

Шаг 2 : Примените Формулу 9.1 для расчета периодической процентной ставки (\ (i_ {Old} \)) для исходной процентной ставки.

Шаг 3 : Примените формулу 9.4 для преобразования в эффективную процентную ставку. При частоте начисления 1 это составляет \ (i_ {New} = IY \) ежегодно начисляемым.

Возвращаясь к сценарию открытия, сравнивая процентные ставки, составляющие 6,6% на полугодовой основе и 6,57% на квартальной основе, необходимо выразить обе ставки в одних и тех же единицах.Следовательно, вы можете преобразовать обе номинальные процентные ставки в эффективные.

	6,6% начисляется каждые полгода	6,57% начислено ежеквартально
Шаг 1	\ (IY = 6,6%; CY_ {Старый} = 2; CY_ {Новый} = 1 \)	\ (IY = 6.57%; CY_ {Старый} = 4; CY_ {Новый} = 1 \)
Шаг 2	\ (i_ {Старый} = 6.{4/1} — 1 = 6,7336% \)

По ставке 6,6%, начисленной раз в полгода, эффективно начисляется 6,7089%, а по ставке 6,57%, начисляемой ежеквартально, — 6,7336%. Лучшая ставка по ипотеке — 6,6%, начисляемая раз в полгода, так как это приводит к ежегодному снижению процентных ставок.

Важные примечания

Калькулятор Texas Instruments BAII Plus имеет встроенный конвертер эффективных процентных ставок под названием ICONV, расположенный на второй полке над кнопкой с цифрой 2.Чтобы получить к нему доступ, нажмите 2-й значок ICONV. Вы получаете доступ к трем входным переменным с помощью кнопок прокрутки ↑ или ↓. Используйте эту функцию, чтобы найти любую из трех переменных, а не только эффективную ставку.

Переменная	Описание	Алгебраический символ
НОМ	Номинальная процентная ставка	\ (IY \)
ЭФФ	Эффективная процентная ставка	\ (i_ {New} \) (годовая сумма)
К / У	Частота соединения	\ (CY \)

Чтобы использовать эту функцию, введите две из трех переменных, вводя каждый фрагмент данных и нажимая ENTER, чтобы сохранить его.Когда вы будете готовы найти неизвестную переменную, прокрутите, чтобы вывести ее на свой дисплей, и нажмите CPT. Например, используйте эту последовательность, чтобы найти эффективную ставку, эквивалентную номинальной ставке 6,6%, начисляемой каждые полгода:

\ [2 \ mathrm {nd} \ text {} \ mathrm {ICONV}, 6.6 \ text {Enter} \ uparrow, 2 \ text {Enter} \ uparrow, \ mathrm {CPT} \ nonumber \]

\ [\ text {Ответ:} 6.7089 \ nonumber \]

Пути к успеху

Ежегодные сложные процентные ставки можно использовать, чтобы быстро ответить на распространенный вопрос: «Сколько времени нужно, чтобы мои деньги удвоились?» Правило 72 — это эмпирическое правило, гласящее, что 72%, разделенные на ежегодно начисляемую ставку доходности, приблизительно соответствуют количеству лет, необходимых для удвоения денег.Написано алгебраически, это

\ [\ text {Приблизительные годы} = \ dfrac {72 \%} {IY \ text {ежегодно}} \ nonumber \]

Например, деньги, инвестируемые под 9% годовых, удваиваются примерно за \ (72 \ div 9 \% = 8 \) лет (фактическое время составляет 8 лет и 15 дней). В качестве альтернативы, деньги, инвестируемые под 3% годовых, удваиваются примерно за \ (72 \ div 3 \% = 24 \) лет (фактическое время составляет 23 года и 164 дня). Обратите внимание на то, насколько приближены значения к фактическому времени.

Упражнение \ (\ PageIndex {1} \): подумайте

заимствования?

Если для удвоения одной инвестиции требуется 36 лет, а для другой — 18 лет, какая эффективная ставка выше?

Ответ

Эффективная ставка равна номинальной ставке или превышает ее.
1. 9%. так как больше процентов заработано
2. 8%, так как проценты выплачиваются меньше
Восемнадцать лет, так как более высокая ставка требует меньше времени на удвоение

Пример \ (\ PageIndex {1} \): понимание ваших инвестиций

Если ваша инвестиция приносит прибыль 5.5% ежемесячно, какова эффективная процентная ставка? В соответствии с Правилом 72, сколько примерно времени потребуется вашим инвестициям, чтобы удвоиться при этой эффективной ставке?

Решение

Рассчитайте эффективную процентную ставку (\ (i_ {New} \)). Как только это станет известно, примените Правило 72, чтобы приблизительно рассчитать время удвоения.

То, что вы уже знаете

Шаг 1 :

Исходная номинальная процентная ставка и начисление сложных процентов вместе с новым начислением сложных процентов известны: \ (IY = 5.5%; CY_ {Old} \) = ежемесячно = 12; \ (CY_ {New} \) = 1

Как добраться

Шаг 2 :

Примените Формулу 9.1 к исходной процентной ставке.

Шаг 3 :

Применяйте формулу 9.4, где \ (i_ {New} = IY \) ежегодно.

Шаг 4 :

Чтобы приблизительно ответить, сколько времени потребуется, чтобы деньги удвоились, примените Правило 72.

Выполнить

Шаг 2 :

\ [i_ {Old} = \ dfrac {5.{\ frac {12} {1}} — 1 = 0,056408 = 5,6408 \% \ nonumber \]

Шаг 4 :

\ [\ text {Приблизительные годы} = \ dfrac {72 \%} {5.6408 \%} = 12.76 \ nonumber \]

Инструкции к калькулятору

2-й значок

НОМ	С / У	EFF
5,5	12	Ответ: 5.640786

Вы фактически зарабатываете 5.6408% годовых. При такой процентной ставке для удвоения основной суммы долга потребуется примерно 12¾ лет, или 12 лет и 9 месяцев.

Пример \ (\ PageIndex {2} \): ваш автокредит

Когда вы ищете ссуду на покупку автомобиля, все банки указали вам ежемесячные комбинированные ставки (которые типичны для автокредитов), самая низкая из которых составляет 8,4%. На вашей последней остановке агент кредитного союза говорит, что, взяв у него автокредит, с вас будет взиматься 8,65%. Что лучше: ссуду в банке или ссуду кредитного союза?

Решение

Так как ссуда на покупку автомобиля начисляется ежемесячно, это нормально, преобразовать эффективную ставку в ежемесячную ставку (\ (IY \)), чтобы она соответствовала всем другим котировкам.

То, что вы уже знаете

Шаг 1 :

Эффективная ставка и начисление сложных процентов следующие: \ (i_ {New} = 8,65%; CY_ {Old} \) = ежемесячно = 12; \ (CY_ {New} \) = 1

Как добраться

(Примечание: в этом случае известен \ (i_ {New} \), поэтому процесс обратный, чтобы прийти к \ (IY \). Таким образом, шаги 2 и 3 выполняются в обратном порядке.)

Шаг 2 :

Замена в Формуле 9.{1/12} = 1 + i_ {Old} \\ & 1.006937 = 1 + i _ {\ text {Old}} \\ & 0.006937 = i _ {\ text {Old}} \ end {align} \ nonumber \ ]

Шаг 3 :

\ [\ begin {выровнено} 0,006937 & = \ dfrac {IY} {12} \\ IY & = 0,083249 \ text {или} 8,3249 \% \ end {выровнено} \ nonumber \]

Инструкции к калькулятору

2-й значок

НОМ	С / У	EFF
Ответ: 8.324896	12	8,65

Предложение кредитного союза в размере 8,65% фактически эквивалентно 8,3249% ежемесячно начисленных процентов. Если самая низкая ставка банков составляет 8,4% ежемесячно, предложение кредитного союза является лучшим выбором.

Эквивалентные процентные ставки

Иногда вам необходимо преобразовать номинальную процентную ставку в другую номинальную процентную ставку, которая не является эффективной. Например, в начальном сценарии этого раздела все ваши ипотечные ставки указывались раз в полгода, за исключением одной месячной ставки.Один из способов сравнить эти ставки — сделать их все эффективными. Альтернативный вариант — взять «чудаковатый» коэффициент и преобразовать его в соответствие со всеми остальными ставками. Это вызывает концепцию эквивалентных процентных ставок, которые представляют собой процентные ставки с разными сложными процентами, которые дают одинаковую эффективную ставку и, следовательно, равны друг другу. Через год две эквивалентные ставки имеют одинаковую будущую стоимость.

Как это работает

Для пересчета номинальных процентных ставок новая формула не требуется.Вместо этого вы вносите незначительные изменения в процедуру эффективной процентной ставки и добавляете дополнительный шаг. Выполните следующие действия, чтобы рассчитать любую эквивалентную процентную ставку:

Шаг 1 : Для номинальной процентной ставки, которую вы конвертируете, определите номинальную процентную ставку (IY) и частоту начисления сложных процентов (\ (CY_ {Old} \)). Также укажите новую частоту начисления сложных процентов (\ (CY_ {Old} = 1 \)).

Шаг 2 : Примените Формулу 9.1 для расчета исходной периодической процентной ставки (\ (i_ {Old} = 1 \)).

Шаг 3 : Примените Формулу 9.4 для расчета новой периодической процентной ставки (\ (i_ {New} \)).

Шаг 4 : Примените Формулу 9.1, используя \ (i_ {New} \) и \ (CY_ {New} \), переставьте и найдите новую конвертированную номинальную процентную ставку (\ (IY \)). {4 \ div 2} -1 = 0.033119 \)

Шаг 6 : Применение формулы 9.1, \ (0,033119 = \ dfrac {I Y} {2} \) или \ (IY = 0,06624 \).

Таким образом, 6,57% начисленных процентов за квартал эквивалентны 6,624%, начисленным за полугодие. Выберите ставку по ипотеке в размере 6,6%, начисляемую раз в полгода, поскольку это самая низкая доступная ставка. Конечно, это то же самое решение, которое вы приняли ранее.

Важные примечания

Преобразование номинальных курсов на калькуляторе BAII Plus выполняется в два этапа:

Шаг 1 : Преобразуйте исходную номинальную ставку и начисление сложных процентов в эффективную ставку.Введите NOM и C / Y, затем вычислите EFF.

Шаг 2 : Введите новое значение C / Y и вычислите NOM.

В приведенном выше примере ставки по ипотеке используйте следующую последовательность:

\ [2 \ text {nd ICONV}, 6.57 \ text {Enter} \ uparrow, 4 \ text {Enter} \ uparrow, \ text {CPT} \ downarrow, 2 \ text {Enter} \ downarrow, \ text {CPT } \ nonumber \]

\ [\ text {Ответ:} 6.623956 \ nonumber \]

Хороший способ запомнить эту технику — не забывать «сначала подниматься, а затем спускаться по лестнице».«Чтобы преобразовать номинальную ставку в эффективную, дважды нажмите« \ (\ uparrow \) ». Чтобы преобразовать эффективную ставку обратно в номинальную, дважды нажмите« \ (\ downarrow \) ». Следовательно, вы идете вверх-вниз по лестнице!

Что нужно остерегаться

При пересчете процентных ставок наиболее распространенный источник ошибок заключается в том, что путают два значения частоты начисления сложных процентов, или \ (CY \). При выполнении шагов четко различите старое сложное соединение (\ (CY_ {Old} \)), из которого вы хотите преобразовать, и новое сложное соединение (\ (CY_ {New} \)), в которое вы хотите преобразовать.Небольшое дополнительное время, потраченное на повторную проверку этих значений, поможет избежать ошибок.

Упражнение \ (\ PageIndex {2} \): подумайте

Если вы конвертируете квартальную ставку в месячную, будет ли конвертированная номинальная ставка выше или ниже?

Ответ

Высшее. Проценты зачисляются на счет реже, поэтому каждый раз нужно вносить больше процентов.
Нижний. Проценты зачисляются на счет чаще, поэтому каждый раз требуется меньше процентов.

Пример \ (\ PageIndex {3} \): какие инвестиции выбрать?

Вы рассматриваете три различных инвестиционных проекта с процентной ставкой 7,75%, начисленные за полгода, 7,7% за квартал и 7,76%, начисленные за полугодие. Какие инвестиции предлагают самую высокую процентную ставку?

Решение

Обратите внимание, что две из трех процентных ставок начисляются раз в полгода, а только одна — ежеквартально. Хотя вы можете преобразовать все три ставки в эффективные ставки (для чего потребуется три расчета), проще преобразовать квартальную ставку с начислением сложных процентов в ставку, начисляемую за полугодие.Затем все ставки суммируются раз в полгода и, следовательно, сопоставимы.

То, что вы уже знаете

Шаг 1 :

Исходная процентная ставка и начисление сложных процентов известны: \ (IY \) = 7,7%; \ (CY_ {Old} \) = ежеквартально = 4; \ (CY_ {New} \) = раз в полгода = 2

Как добраться

Шаг 2 :

Примените Формулу 9.1 к исходной процентной ставке.

Шаг 3 :

Преобразуйте исходную процентную ставку в новую периодическую ставку, используя Формулу 9.{4 \ div2} -1 = 0,038870 \ nonumber \]

Шаг 4 :

\ [\ begin {выровнено} 0,038870 & = \ dfrac {IY} {2} \\ IY & = 0,077741 \ text {или} 7,7741 \% \ end {выровнено} \ nonumber \]

Инструкции к калькулятору

2-й значок

Ступени	НОМ	С / У	EFF
1-3	7,7	4	Ответ: 7.925204
4-6	Ответ: 7.774112	2	\ (\ surd \)

Квартальная начисленная ставка в размере 7,7% эквивалентна 7,7741%, начисляемая каждые полгода.

Эффективная процентная ставка | Формула | Расчет

Определение

Формула

Примеры расчета

Пример 1

Пример 2

Пример 3

Функция НОМИНАЛ — Служба поддержки Office

Описание

Синтаксис

Замечания

Пример

Функция ЭФФЕКТ — Служба поддержки Office

Описание

Синтаксис

Замечания

Пример

Эффективная ставка по кредиту

Эффективная, номинальная, реальная ставка по кредиту – отличия

Номинальная процентная ставка

Что в нее входит

Что в нее НЕ входит

Нужно ли ее принимать в расчет

При чем тут инфляция

Реальная процентная ставка

Что в нее входит

Что в нее НЕ входит

Нужно ли ее принимать в расчет

Когда это важно для кредита

Эффективная процентная ставка (ЭПС)

Что в нее входит

Что в нее НЕ входит

Как ее узнать

Действительно ли ПСК является полной

Сколько придется платить в конечном итоге

Понятие, формула и расчет эффективной ставки по вкладу

Понятие и сущность

Зачем на практике ее высчитывать

Формула и примеры ее использования

Что изменится, если пополнить или частично снять деньги со вклада

Рекомендации вкладчикам

Определение эффективной годовой процентной ставки

Что такое эффективная годовая процентная ставка?

Эффективная годовая процентная ставка

О чем говорит эффективная годовая процентная ставка?

Ключевые выводы

Пример эффективной годовой процентной ставки

Более частое начисление сложных процентов дает более высокую прибыль

Пределы компаундирования

Часто задаваемые вопросы

Какова эффективная годовая процентная ставка?

Как рассчитать эффективную годовую процентную ставку?

Почему важна эффективная годовая процентная ставка?

Эффективная годовая ставка — определение, формула, что вам нужно знать

Что такое эффективная годовая ставка?

Калькулятор эффективной годовой ставки

Скачать бесплатный шаблон

Калькулятор эффективной годовой ставки

Что такое номинальная процентная ставка?

Что такое комплексный период?

Подробнее о процентных ставках

Насколько важна эффективная годовая ставка в бизнесе?

Дополнительное обучение

Эффективная годовая ставка (EAR) — Как рассчитать эффективную процентную ставку

Что такое эффективная годовая процентная ставка?

Эффективная годовая ставка на основе начисления сложных процентов

Важность эффективной годовой ставки

EAR Пример

Скачать бесплатный шаблон

Калькулятор эффективной годовой процентной ставки

Как рассчитать эффективную процентную ставку?

1.Определите заявленную процентную ставку

2. Определите количество периодов начисления сложных процентов

3 .Примените формулу EAR: EAR = (1+ i / n)

Пример

Почему банки не используют эффективную годовую процентную ставку?

Дополнительная литература

Как рассчитать эффективную процентную ставку — AccountingTools

Связанные курсы

Как рассчитать эффективную годовую процентную ставку