Эффективная годовая процентная ставка.

⇐ ПредыдущаяСтр 4 из 11Следующая ⇒

Различные виды финансовых контрактов могут предусматривать различные схемы начисления процентов. Как правило, в этих контрактах обычно оговаривается номинальная процентная ставка, которая не принимает во внимание изменение стоимости денег в связи с инфляцией.

Номинальная процентная ставка имеет следующие недостатки:

1) она не отражает реальной эффективности сделки;

2) в связи с этим она не может быть использована для сопоставления эффективности различных инвестиционных проектов.

Поэтому, для обеспечения сравнительного анализа эффективности таких контрактов применяется другой показатель, который является универсальным для любой схемы начисления процентов.

Таким показателем является эффективная годовая процентная ставка 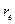, которая обеспечивает переход от PV к FV при заданной годовой процентной ставке и однократным начислением процентов.

Общая постановка задачи формулируется следующим образом.

Задана исходная сумма PV, номинальная процентная ставка r и количество начислений сложных процентов m.

Естественно, что этому набору исходных величин в рамках одного года соответствует вполне определенное значение будущей стоимости FV.

Требуется найти такую годовую ставку 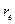, которая обеспечила бы точно такое же наращение, как и исходная схема, но при m = 1. Т.е. обе схемы должны быть равносильными.

В рамках одного года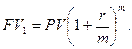

Из определения годовой эффективной ставки вытекает, что:

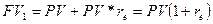, откуда .

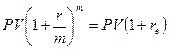Разделив обе части равенства на PV получим:

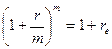. Откуда .

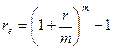Из полученной формулы видно, что эффективная ставка зависит от количества внутригодовых начислений, причем с ростом m она увеличивается. Кроме того, для каждой номинальной ставки можно найти соответствующую ей эффективную ставку. Эти две ставки совпадают при m = 1. Именно годовая эффективная процентная ставка является критерием эффективности финансовых операций и может быть использована для пространственно-временных сопоставлений.

Пример.

Предприниматель может получить ссуду на следующих условиях:

а) либо исходя из ежемесячного начисления процентов по номинальной процентной ставке 26% годовых;

б) либо исходя из полугодового начисления из расчета 27% годовых.

Какой вариант предпочтительнее?

а)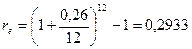

б)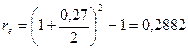

Так как эффективная годовая процентная ставка характеризует относительные расходы предпринимателя по обслуживанию ссуды, то вариант б) для предпринимателя более предпочтителен. Необходимо также отметить, что принятие решения не зависит от величины кредита, поскольку критерием является относительный показатель – эффективная процентная ставка.

Понимание роли эффективной процентной ставки чрезвычайно важно для финансового менеджера. Дело в том, что принятие решения о привлечении средств, например банковской ссуды на тех или иных условиях, делается чаще всего исходя из приемлемости предполагаемой процентной ставки, которая в этом случае характеризует относительные расходы заемщика. В рекламных проспектах непроизвольно или умышленно внимание на природе ставки обычно не акцентируется, хотя в подавляющем числе случаев речь идет о номинальной ставке, которая может весьма существенно отличаться от эффективной ставки.

Пример.

Рассчитать эффективную годовую процентную ставку при различной частоте начисления процентов, если номинальная ставка равна 10%.

M
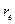
	0,10	0,1025	0,10381	0,10471	0,10516

Различие между двумя ставками может быть гораздо более может быть гораздо более разительным при заключении некоторых специальных кредитных договоров, например, при оформлении кредита на условиях добавленного процента.

В финансовых соглашениях не имеет значения, какую из ставок указывать – эффективную или номинальную, поскольку использование как одной, так и другой дает одну и ту же наращенную сумму. В США в практических расчетах применяют номинальную ставку. В европейских странах, как правило, вначале определяется эффективная ставка, а затем используется формула .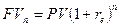

Если в контракте указаны эффективная ставка и количество начислений сложных процентов, а необходимо найти номинальную ставку, то используется формула:

.

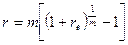Пример.

Определить номинальную ставку, если эффективная ставка равна 18% и сложные проценты начисляются ежемесячно.

.

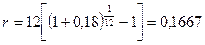Таким образом, ежегодное начисление сложных процентов по ставке 18% годовых дает какой же результат, что и ежемесячное начисление сложных процентов по ставке 16,67%.

Если две номинальные годовые процентные ставки определяют одну и ту же эффективную ставку, то они называются эквивалентными.

Пример.

Каковы будут эквивалентные номинальные годовые процентные ставки с начислениями по полугодиям и ежеквартально, если соответствующая им эффективная ставка равна 20%?

для полугодового начисления ;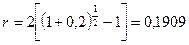

для ежеквартального начисления .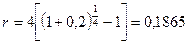

Таким образом, номинальные ставки 19,09% и 18,65% являются эквивалентными.

Мы рассмотрели наиболее стандартный и широко распространенный подход к понятию эффективной ставки.

Однако, возможны и другие подходы, которые вытекают из разнообразия финансовых соглашений. Например, вполне реальна ситуация, когда условия начисления процентов меняются: в частности, после схемы сложных процентов начиная с какого то момента времени начинают использовать схему простых процентов без прерывания действия контракта. Для анализа таких ситуаций может быть предложен следующий подход к нахождению эффективной процентной ставки. Пусть известна первоначальная сумма PV и наращенная каким либо образом за время n сумма FV. Тогда по определению:

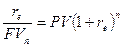и поэтому .

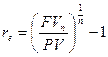Пример.

В долг на 2,5 года предоставлена сумма в 30 тыс. грн. с условием возврата 40 тыс. грн. Найти эффективную ставку в этой финансовой сделке.

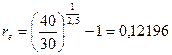или 12,196%.

Проверим полученный результат. Предположим в банк помещен вклад в размере 30 тыс. грн. на 2,5 года под 12,196% годовых сложных процентов. Тогда наращенная сумма будет равна:

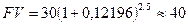тыс. грн.

Как и в случае процентной ставки можно также определить эффективную годовую учетную ставку 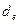. Она обеспечивает переход от к при заданных значениях этих параметров и однократном дисконтировании в течение года.

Поскольку согласно определению в рамках одного года

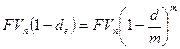, то после соответствующих преобразований получим: .

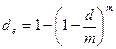Из приведенной формулы следует, что с ростом количества начислений величина годовой учетной ставки уменьшается.

Зная годовую учетную ставку можно определить коэффициент дисконтирования: .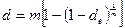

Используя 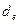можно определить эквивалентные номинальные учетные ставки.

Эффективную годовую учетную ставку можно определить иначе, если известна величина 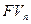, и дисконтированная каким-либо образом за время 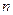сумма .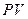

В этом случае 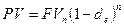, откуда .

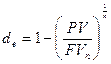Пример.

Долговое обязательство равное 5 тыс. грн. со сроком погашения 4 года было сразу же учтено в банке и владелец обязательства получил 4,2 тыс. грн.

Найти эффективную годовую учетную ставку.

Тема 4



Временная стоимость денег — zpv_sib — LiveJournal

Эффективная годовая процентная ставка (The Effective Annual Rate)

Годовая процентная ставка – это заявленная ставка, под которой понимается то , что проценты будут выплачены 1 раз в год. Однако на практике часто встречаются условия с выплатой сложных процентов – например, проценты выплачиваются ежеквартально, ежемесячно, ежедневно или вообще непрерывно, при этом проценты. Для того чтобы сравнивать процентные ставки по различным инструментам, с учётом различий в периодах начисления процентов, необходимо приводить все ставки к единой базе. Эффективная годовая доходность отражает фактический уровень доходности, с учётом всех периодов выплаты процентов внутри одного года. Эффективная годовая процентная ставка (EAR) рассчитывается по формуле:

 
Эффективная годовая процентная ставка (EAR) = (1 + процентная ставка периода) ^m — 1,%

где : m = количество периодов начисления процентов
        процентная ставка периода = заявленная ставка / m

Например:

Заявленная годовая ставка 9%, проценты начисляются ежемесячно методом сложного процента, тогда эффективная годовая ставка будет:

EAR = (1 + (0,09/12)) 12 — 1 = (1,0075) 12 — 1 = (1,093807) — 1 = 0,093807 или 9,38%

Понятно, что чем больше периодов начисления процентов тем больше будет EAR, и если m>1 то эффективная ставка всегда выше заявленной.

Решение кейсов на базе временной стоимости денег.

Введём понятия PV (presnt value) и FV (future value) нынешняя стоимость и будущая стоимость денег. Если задана годовая ставка, и имеются данные о периодах начисления процентов, то определить будущую стоимость можно поделив годовую ставку на количество периодов начисления процентов в году и возвести в степень равную количеству периодов умноженному на количество лет.

Например:

Необходимо определить будущую стоимость $10 000 при ставке в 8% годовых через 5 лет, с периодом начисления раз в месяц. Ставка для расчёта по формуле будет r=8/12 = 0.0067%, а количество периодов N = 12* 5 = 60.

FV = PV * (1 + 0.0067) ⁶⁰ = $14 928

Обязательно перед решением подобных кейсов приводите периоды начисления N и процентную ставку r в к единым измерениям!

Текущая стоимость перпетуитета (бесконечного потока платежей).

Перпетуитет начинается как обычный аннуитет (первый денежный поток является единственным и начинается с текущего момента), но не имеет конца и продолжается бесконечно,- одним и тем же платежом последовательно в каждом периоде. Казалось бы какой смысл? Какая организация обяжет себя платить бесконечно? Однако некоторые ценные бумаги, например привелигированные акции, выпускаются в предположении что предприятие будет работать вечно, а значит и вечно выплачивать фиксированный платёж. Формула текущей стоимости бесконечного потока платежей является отправной точкой для оценки такого рода бумаг.

Упрощённо можно рассчитать так:

PV перпетуитета = аннуитетный платёж (А)
                                   годовую процентную ставку (r)

Например:

Бесконечный перпетуитет $1000 при ставке в 8% , текущая стоимость такого перпетуитета будет равна 1000/0,08 = $12 500

Упрощения и допущения: N – Стремится в бесконечность, ставка положительна.

FV и PV одинарного денежного потока.При условии выплаты процента ежегодно, текущую и будущую стоимость одинарного аннуитета можно посчитать:

         (1) FV = PV * (1 + r)^N

          (2) PV = FV *      {      1     }
                                       (1 + r)^N

где: FV = будущая стоимость,
PV = текущая стоимость, R = годовая процентная ставка,
and N = количество лет.

Поупражняемся:

Если я открываю депозит $5000 на 5 лет с ежегодным начислением процентов, по ставке 12%, то на пятый год я получаю: 5000 * (1,12) в 5 степени = $8811,7

Или наоборот, хочу 1 000 000 через 20 лет, сколько нужно положить на депозит сейчас при ставке в 6% годовых, 1 00 000 * [1/(1,06) в степени 20] = 311 800  , т.е. сегодняшняя стоимость 1 млн долларов через 20 лет при ставке 6% составляет 311 800.

Что дает эффективная годовая процентная ставка

Эффективные процентные ставки существуют для вкладов и для кредитов. Разбираться в банковских терминах необходимо, чтобы проводить осознанный выбор выгодных условий и операций. Узнайте, что такое эффективная процентная ставка.

Эффективная годовая процентная ставка

Очень часто в описании банковских продуктов можно встретить такой термин, как эффективная процентная ставка. Зачастую этот показатель является одним из ключевых, когда идёт выбор банка, услугами которого люди хотят воспользоваться.

Но, при этом, далеко не все до конца понимают, в чём суть подобной ставки и почему она играет такую важную роль. В этом стоит внимательно разобраться, чтобы в дальнейшем не было никаких подвохов, чтобы можно было ориентироваться на настоящие, а не только на рекламируемые величины.

Эффективная процентная ставка по вкладу

Эффективные процентные ставки могут существовать как для вкладов, так и для кредитов. В первом случае это прямая противоположность номинальной ставке, начисляемая при капитализации процентов. Если имеется лишь номинальная ставка, то вкладчик вносит деньги на банковский счёт, в конце срока на них начисляются определённые проценты, которые он получает затем на руки или на счёт. При эффективной ставке заемщик не получает проценты на руки, пока срок действия вклада не окончен.

Вместо этого прибыль кладётся на счёт его депозита. Таким образом, месяц от месяца общая сумма вклада постепенно начинает возрастать. А раз она возрастает, то увеличиваются и набегающие в итоге проценты. Вкладчик получает больше денег, чем при номинальной ставке, если продолжительность вкладов при этом будет одинакова. В банковском договоре данную ставку могут назвать также доходом с учётом капитализации или доходом с учётом сложного процента.

Эффективная процентная ставка по кредиту

Отличается по своей сути эффективная ставка по кредиту. От неё напрямую зависит полная стоимость кредита – потому иногда её также называют «полной стоимостью кредита». Важно сравнивать именно эффективные процентные ставки, чтобы получить максимально реалистичное представление о том, какие денежные суммы будут уплачены при том или ином кредите.

Ранее данная ставка могла оставаться на совести банка, но в настоящее время Центробанк настоятельно велел кредитным организациям доводить до вкладчиков настоящую стоимость кредита ещё до того, как будет заключен договор, то есть, фактически, ещё на этапе консультации. Но всё же не все люди обращают достаточное внимание на подобные нюансы, а потом выходит, что они переплачивают по кредитам больше, чем того хотели бы.

Когда банки заявляют о процентах, которые заемщики должны выплатить по кредиту, они умалчивают, что присутствовать будут и дополнительные расходы, которые могут увеличить затраты и общую ставку. Если же рассматривать эффективную процентную ставку, то все эти вещи в её рамках будут учитываться.

Что же включается в эффективную процентную ставку? В неё входят:

• платежи по погашению годовых процентов и основного долга;
• комиссия на выдачу кредита и рассмотрение заявки;
• плата за операционное и расчетное обслуживание;
• плата за открытие и ведение ссудного счёта;
• страхование заемщика или предмета залога;
• регистрация и оценка залога;
• и ряд других платежей.

Все платежи, которые напрямую вытекают из кредитного договора и имеют обязательный характер являются частью эффективной процентной ставки по кредиту. Важно понимать, что в подобную ставку не входит. Не входят в неё платежи, которые относятся к штрафным санкциям за неисполнение кредитных обязательств, также не входят в неё платежи, которые могут либо произойти, либо нет, в зависимости от того, какую линию поведения изберёт заемщик.

Если человек пользуется кредитной картой, то эффективная процентная ставка также имеется, но достаточно эффективной картины она нам не даёт, потому что пользование кредитной картой напрямую зависит от заемщика – он может осуществлять снятие денег и выплату в произвольном порядке, потому условно принимается, что заемщик пользовался на протяжении максимального периода действия всем предоставленным ему размером лимита, а долг погашал равномерными платежами, что, конечно, не так уж часто происходит в действительности.

В любом случае, берёте ли вы кредит, или же делаете вклад, чтобы лучше контролировать свои денежные средства, необходимо знать, какова эффективная процентная ставка.

© Сергей, BBF.RU

Эффективная годовая процентная ставка: расчет и формула

Содержание

Каждый человек, который в своей жизни оформлял кредит, знает, что означает эффективная годовая процентная ставка. Она представляет собой полную стоимость кредита, а на этот критерий нужно обязательно обращать много внимания в процессе оформления кредита, который может быть получен на приобретение квартиры или машины, а также сюда относится кредит на образование или на развитие бизнеса. Дело в том, что именно от годовой ставки зависит то, выгодный ли будет кредит для заемщика, а также какую сумму в конечном итоге ему придется выплатить банку.

Особенности эффективной годовой ставки

В процессе оформления любого кредита важно помнить, что нередко банки в процессе рекламы своих кредитных продуктов не раскрывают то, какая ставка при этом будет использоваться. Дело в том, что добавочные затраты, как правило, открываются именно при оформлении кредита. За счет этого процентная ставка существенно увеличивается, что не является уже выгодным для клиентов. Именно поэтому расчет эффективной ставки процента должен производиться каждым потенциальным заемщиком предварительно, чтобы он точно знал, какая ставка будет применяться, а также какова будет переплата за кредит. Только тогда можно правдиво и достоверно изучить стоимость всего кредита и определиться, является ли он выгодным.

В процессе расчета важно учитывать все платежи, которые должны быть оплачены заемщиком в период оформления кредита, а также в течение его выплаты. Сюда должны входить всевозможные комиссии и дополнительные сборы, расходы на обслуживание или на открытие счета, а также другие затраты. Нельзя забывать о тех деньгах, которые должен тратить заемщик при страховании различных рисков, к которым в первую очередь относится риск потери трудоспособности. Однако не следует в процессе расчета учитывать те затраты, которые должен понести должник в том случае, если в течение выплаты кредита нарушит какие-либо условия договора, а именно будет обнаружена просрочка выплаты, поскольку тогда начисленные пени и штрафы не входят в эффективную ставку.

Как правильно рассчитывается эффективная годовая процентная ставка

Для расчета данного показателя используется формула сложных процентов. Однако здесь важно помнить, что насчет процентов осуществляется с помощью простых процентов, поэтому даже без наличия каких-либо дополнительных комиссионных отчислений по кредиту может сложиться такая ситуация, когда эффективная ставка будет намного выше, чем ставка по кредиту, которая указывается банком. Для расчета рекомендуется использовать Microsoft Excel, в котором имеется специальная функция – ЧИСТВНДОХ, а расчет является очень простым, поскольку достаточно только ввести некоторые данные, к которым в первую очередь относятся временные рамки выплат по кредиту.

Однако сегодня каждый банк обязан по запросу потенциального заемщика предоставлять информацию о том, какой является эффективная годовая процентная ставка. Это необходим для того, чтобы человек при поиске банка, который будет предлагать самые лучшие условия кредитования, не тратил много сил и времени на то, чтобы для каждого возможного варианта определять данный показатель. Также сегодня многие современные банки, которые имеют собственный сайт в интернете, располагают на этом ресурсе специальные онлайн калькуляторы, с помощью которых каждый клиент может точно узнать все необходимые цифры по различным кредитам.

Какие факторы влияют на эффективную ставку?

Для правильного расчета данного показателя важно учитывать и множество факторов, которые оказывают на него непосредственное воздействие. Поэтому важно помнить о том, какой именно выбран вид платежа, поскольку он может быть аннуитетным или дифференцированным, а также может быть выбран буллитный платеж. Дополнительно учитывается, каков первоначальный взнос со стороны заемщика, а также нужно помнить о периодичности платежей. Расчеты, которые проводятся для разных сроков кредитования, могут иметь существенные отличия.

Форма оплаты является самым важным фактором, который нужно учитывать в процессе расчета эффективной годовой процентной ставки. Важно знать, в чем состоят отличия различных видов платежей. Если выбран аннуитетный платеж, то все взносы будут одинаковыми за весь период выплаты кредита. При оформлении дифференцированного кредита размер ежемесячных платежей будет уменьшаться по мере выплаты кредита. Буллитный платеж предполагает, что изначально заемщиком полностью погашаются проценты по кредиту, а только потом начинается выплата основного долга. Самым выгодным считается дифференцированный платеж, однако он является и самым сложным в плане выплаты, поскольку сразу после оформления кредита придется уплачивать ежемесячно очень большие деньги.

Таким образом, каждый человек, который планирует оформить довольно существенный кредит, который предназначен для покупки дорогостоящих элементов или для оплаты обучения, должен знать, как правильно рассчитывать эффективную годовую процентную ставку, для чего она нужна, как ее сравнить в различных вариантах кредитования, а также как грамотно с ее помощью выбрать самый оптимальный и выгодный кредит в банке. В этом случае можно рассчитывать на то, что заемщик оформит кредит под хорошие проценты, а при этом не будет дополнительных ненужных переплат и комиссионных сборов.

Эффективная годовая процентная ставка: особенности и расчет

Добавлено в закладки: 0

Эффективная процентная ставка или полная стоимость кредита –  знакомое понятие для тех, кто оформлял ипотечный кредит, кредит на автомобиль, займ на образование или на развитие малого бизнеса. Клиенты обращают на это внимание, когда начинают сравнивать условия по кредитным займам в различных банках.

Центробанк, осуществляя контролирование над деятельностью учреждений, занимающихся кредитованием, вменил в обязанность  доводить данную  информацию до посетителей в обязательном порядке. Такого рода  сведениями кредитозаемщик должен владеть на первоначальном этапе до подписания сделки.

Суть эффективной ставки

Объявленные банком в рекламных продуктах расчеты по кредитам, не всегда соответствуют действительности. Очень часто в них не упоминаются добавочные затраты для заемщика. Данные  издержки порой сильно повышают затраты по кредиту, увеличивая процентную ставку за счет дополнительных функций: прием платежей, выдачу и закрытие кредита.

Чтобы избежать излишних переплат, которые  всплывут  при  добавочных сборах и комиссиях, и с целью дать правдивую оценку стоимости кредита,осуществляется расчет эффективной годовой процентной ставки.  Начиная составление договора  предстоящего кредита, стоит помнить, что в момент расчета ставки суммируются выплаты всех направлений: комиссия за разбор заявки, выдача кредита, расчетное и операционное  обслуживание, открытие кредитного счета и его ведение, погашение кредитного займа  и процентов по нему.

Сюда же, включают и  все страховые риски в интересах третьего лица, расходы, понесенные в процессе оформления залога и его оценка. Включаются все платежи, носящие обязательный характер и следующие из договора.

В расчеты эффективной ставки не войдут лишь платежи, которые сопряжены с неисполнением каких-либо обязательств и поведением заемщика. Бывают случаи, когда появляется возможность преждевременного закрытия задолженности. Если условиями договора за это предусмотрены штрафные санкции, они не станут включаться в расчет. Такое решение принял клиент самостоятельно.

Иная картина складывается при расчете ПСК по банковским кредитным картам. Дать прогноз сложно. За основу берется расчет, как если бы клиент решил пользоваться  полным лимитом на длительный период действия, а долг погашал платежами равномерного характера. Поэтому по кредитным картам эффективная процентная ставка не может быть наиболее высокоэффективной.

Как производится расчет ПСК

Формула расчета годовой процентной ставки  рассчитывается исходя из расчета  сложных процентов. Но вследствие того, что проценты насчитываются  по схеме  простых процентов, велика вероятность, что, даже не имея специальных комиссий по займу, эффективная ставка будет выше, нежели процентная ставка по кредиту. Ставку определяют  с помощью программы Microsoft Excel и ее финансовой функции «ЧИСТВНДОХ». Зная временные рамки выплат платежей по своему кредиту, просчитать ее можно самостоятельно.

Если потребитель будет самостоятельно просчитывать ставку по нескольким банкам, времени и сил будет потрачено много и бессмысленно. Банк должен эту информацию предоставить в любом случае.

Невзирая на то, что определения: эффективная процентная ставка (ЭПС) и полная стоимость кредита (ПСК) фактически обозначают одно и то же, Центральный банк с  июня 2008 г. заставил кредитные организации в безусловном порядке раскрывать ее клиентам ПСК, как только ввел это понятие.

Придя в  банк с целью оформления займа, можно ознакомиться с  полной калькуляцией кредита. Было бы легче сделать это  при обращении напрямую на сайт банка, где с помощью кредитного калькулятора,  можно увидеть данный расчет.

Что воздействует  на ПСК?

На достоверный расчет ПСК влияет много факторов, которые требуется учитывать поверх совершаемых выплат по кредиту. Воздействие окажет вид платежа, который может быть дифференцированным, буллитным или аннуитетным. Также время действия кредита, первичный взнос и периодичность платежей. Чтобы не произошло искажение информации, нужно проводить сравнение  эффективной процентной ставки при одинаковых условиях получения кредитного займа.

Но могут случиться неожиданности, которым находятся объяснения благодаря расчетам ставки. Расчет на год или на 5 лет, при равнозначных условиях, будет отличаться.

Следующий фактор, оказывающий воздействие на ставку – форма оплаты. Оформляя кредит, заемшик подписывает договор, согласно которому будет определен вид платежа.

Существует 3 вида платежей:

• аннуитетный – платежи одинаковы на протяжении всего срока кредитования;
• дифференцированный – размер денежного платежа снижается лишь к концу погашения кредита;
• буллитный – вначале заемщик выплачивает проценты по кредиту, а в конце закрывает сам долг.

Если не вдаваться сильно в подробности, то переплачивать в  случаи дифференцированно расчлененных платежей придется меньше. Вот только что же произойдет с ПСК?

Узнать о реальной переплате снова не удастся. Эффективная ставка будет поменьше при буллитном погашении долга, чуть выше при аннуитетном и высокой при дифференцированном погашении. Отсюда можно сделать вывод, что при выборе кредитной программы, рассматривать и ставить  в одну плоскость условия по эффективной процентной ставке неправильно. Можно подобрать не самый удачный вариант.

4.2.6. Эффективная годовая процентная ставка

Различные
виды финансовых контрактов могут
предусматри­вать различные схемы
начисления процентов. Как правило, в
этих контрактах оговаривается номинальная
процентная ставка, обычно годовая. Эта
ставка, во-первых, не отражает реальной
эффективности сделки и, во-вторых, не
может быть использована для сопоставлений.
Для обеспечения сравнительного анализа
эф­фективности таких контрактов
необходимо выбрать некий пока­затель,
который был бы универсальным для любой
схемы начис­ления. Таким показателем
является эффективная годовая про­центная
ставка r
_e
,
обеспечивающая переход от P
к F
_n

при
заданных значениях этих показателей и
однократном начислении процентов.

Общая
постановка задачи может быть сформулирована
сле­дующим образом. Задана исходная
сумма Р,
годовая процентная ставка (номинальная)
r,
число начислений сложных процентов m
. Этому
набору исходных величин в рамках одного
года соответствует вполне определенное
значение наращенной ве­личины F
₁.
Требуется
найти такую годовую ставку r_e,
которая обеспечила бы точно такое же
наращение, как и исходная схема, но при
однократном начислении процентов, т.е.
m
= 1. Иными словами, схемы {Р
,
F₁
,
r
, m
> 1} и { Р,
F₁
,
r_e
, m
= 1} должны быть равносильными.

Из формулы (4.7)
следует, что в рамках одного года:

F
₁
=
P · (1
+
r/m)^m
.

Согласно определению
эффективной годовой процентной ставки:

F₁
=P
+ P · r_e

=
P · ( 1 + r_e)

отсюда:

r_e

= (1 + r/m)^m
– 1.
(4.13)

Из
формулы (4.13) следует, что эффективная
ставка зависит от количества внутригодовых
начислений, причем с ростом m
она увеличивается. Кроме того, для каждой
номинальной ставки можно найти
соответствующую ей эффективную ставку;
две эти ставки совпадают лишь при m
= 1. Именно ставка r_e

является критерием эффективности
финансовой сделки и может быть
ис­пользована для пространственно-временных
сопоставлений.

Пример

Предприниматель
может получить ссуду а) либо на условиях
ежеквартального начисления процентов
из расчета 75
% годовых,
б) либо на условиях полугодового
начисления процентов из расчета 80
% годовых.
Какой вариант более предпочтителен?

Относительные
расходы предпринимателя по обслуживанию
ссуды могут быть определены с помощью
расчета эффективной годовой процентной
ставки — чем она выше, тем больше уровень
расходов. По формуле (4.13):

вариант
(а)
r
_e
= (1 + 0.75/4)⁴
— 1 = 0,99,

вариант
(б)
r
_e
= (1 + 0,80/2)²
— 1 = 0,96.

Таким
образом, вариант (б) является более
предпочтитель­ным для предпринимателя.
Необходимо отметить, что принятие
решения не зависит от величины кредита,
поскольку критерием является относительный
показатель — эффективная ставка, а она,
как следует из формулы (4.13), зависит лишь
от номиналь­ной ставки и количества
начислений.

Понимание
роли эффективной процентной ставки
чрезвычай­но важно для финансового
менеджера, поскольку принятие реше­ния
о привлечении средств, например,
банковской ссуды на тех или иных условиях,
делается чаще всего исходя из приемлемости
предлагаемой процентной ставки, которая
в этом случае харак­теризует
относительные расходы заемщика. В
рекламных проспе­ктах непроизвольно
или умышленно внимание на природе ставки
обычно не акцентируется, хотя в подавляющем
числе случаев речь идет о номинальной
ставке, которая может весьма сущест­венно
отличаться от эффективной ставки.
Рассмотрим простей­ший пример.

Пример

Рассчитать
эффективную годовую процентную ставку
при различной частоте начисления
процентов, если номинальная ставка
равна 10%. По формуле (4.13):

Различие
между двумя ставками может быть гораздо
более разительным при заключении
некоторых специальных кредитных
договоров, например, при оформлении
кредита на условиях до­бавленного
процента.

А вы знаете, что такое годовая эффективная ставка по кредиту?

Подписывая кредитный договор, человек сталкивается со многими непонятными терминами. Оказывается, в кредитном договоре может быть указана одна процентная ставка, а когда приходится рассчитываться за кредит процентная ставка значительно выше. Существует такое понятие, как кредитная ставка по кредитному договору и эффективная кредитная ставка по кредиту. Эти две величины обозначают разные цифры и могут существенно отличатся.

Процентная ставка по кредиту это процент от суммы кредита, который заемщик будет переплачивать за пользование банковскими деньгами ежемесячно или ежегодно. Но заемщик переплачивает не только проценты по кредиту, он платит за обслуживание кредитного счета, за открытие этого счета, разные одноразовые комиссии, разные страховки, скрытые платежи и другие уплаты. В итоге стоимость кредита получается выше, чем тело кредита плюс проценты за пользование кредитом, насчитанные на весь период кредитования. Указание одной процентной ставки в договоре, и существование отличительной от нее эффективной реальной ставки вызывало возмущение со стороны потребителей. Ведь им изначально было неясно, какая реальная переплата по кредиту. Поэтому, вышел закон, который обязывает банкиров сообщать заемщику эффективную процентную ставку до совершения сделки.

Эффективная процентная ставка по кредиту или полная стоимость кредита включает в себя годовую ставку по кредиту, скрытые платежи, дополнительные комиссии, страховки и одноразовые взносы за обслуживание или открытие счета, разделенные на период оформления кредита. Таким образом, эффективная ставка по кредиту на 10 тысяч сроком на один год будет выше, чем эффективная ставка по кредиту на эту же сумму на пять лет. При этом переплата по кредиту сроком на один год будет значительно ниже, нежели переплата по кредиту сроком на пять лет.

Простая формула расчета годовой эффективной ставки выглядит следующим образом:

ЭПС = ЗС + ЕК * 12 + (ОК + 100% × (ССП + ССОП) / СК) / СрК

Аббревиатура:

ЭПС — реальная годовая ставка.

ЗС — заявленная ставка в кредитном предложении, в процентах.

ЕК — ежемесячная комиссия (за снятие средств или за пользование кредитными средствами), в процентах.

ОК — одноразовая комиссия (чаще всего применяется при выдаче полной суммы кредита), в процентах.

ССП — сумма всех страховых платежей, в денежном выражении.

ССОП — сумма сопутствующих одноразовых платежей (оформление бумаг, РКО, открытие счета, нотариальные услуги и так далее), в денежном выражении.

СК — сумма кредита.

СрК — срок погашения задолженности, в годах.

Несмотря на то, что банкиры сегодня вынуждены называть эффективную процентную ставку по кредиту, сравнивать кредитные программы только по величине эффективной ставки не следует. Эффективная кредитная ставка по кредиту зависит от сроков кредитования и суммы кредита. По одному кредитному договору эффективная ставка будет выше, чем по второму, но выгоднее может быть второй кредитный договор. Чтобы понять в каком банке предоставляют кредит на более выгодных условиях, необходимо сравнивать аналогические кредитные программы. Обе кредитные программы должны быть рассчитаны на одну саму и на такой же срок. Только тогда можно смотреть на эффективную процентную ставку и выбирать тот кредит наличными онлайн, где она получается ниже.

Пример вопроса об эффективной годовой ставке

| CFA Уровень I

Эффективная годовая процентная ставка (EAR) — это норма прибыли, полученная инвестором в год, с учетом эффекта начисления сложных процентов. Помните, что начисление сложных процентов — это процесс, при котором инвестированные средства экспоненциально растут за счет как основной суммы, так и уже накопленных процентов, принося больше процентов. Другими словами, проценты, полученные сами по себе, приносят больше процентов. Математически мы можем определить EAR следующим образом:

$$ \ text {EAR} = \ left (1+ \ text {периодическая ставка} \ right) ^ \ text {m} — 1 $$

Где, \ (\ text {периодическая ставка} = \ frac {\ text {заявленная годовая ставка}} {m} \)

И м — количество периодов начисления сложных процентов в год.{365} -1 = 12,75 \% \\
\ end {align *} $$

Во-первых, вы должны заметить, что по мере увеличения частоты сложения увеличивается и EAR.

Более того, указанная ставка равна EAR только при ежегодном начислении процентов.

Почему так важна эффективная годовая процентная ставка?

EAR — важная концепция в финансовом менеджменте, поскольку она используется для сравнения двух или более проектов, в которых сложный процент рассчитывается по-разному. Предположим, у вас есть два проекта X и Y.Проект X выплачивает 5% начисленных процентов ежемесячно, а проект Y выплачивает 5% начисленных процентов ежеквартально. Посчитав EAR, представленный каждой из этих двух ставок, вы сможете выбрать наиболее прибыльный проект из двух. Кроме того, чем выше EAR, тем выше доход от инвестиций.

Вопрос

Джон Росс, финансовый аналитик, хотел бы сохранить на своем банковском счете 20 000 долларов по истечении 5 лет. Банк предлагает доходность 10% годовых, начисляемую каждые полгода.{-5} = 12 279 долларов США

Чтение 6 LOS 6c

Рассчитайте и интерпретируйте эффективную годовую ставку с учетом указанной годовой процентной ставки и частоты начисления сложных процентов.

.

годовая процентная ставка | Процентные ставки

Если бы у нас все было по-своему, мир финансов был бы простым и легким местом. К сожалению, есть много вещей, которые вам нужно изучить и учесть, прежде чем делать ставку на свои деньги. Одна из них — ваша процентная ставка. Но подождите — существуют разные виды процентных ставок, и важно, чтобы вы их исправили, когда ищете наиболее выгодную сделку.

Какая годовая процентная ставка?

Годовая процентная ставка, иногда называемая стандартной годовой процентной ставкой или базовой ставкой, — это процентное значение, которое вы обычно видите в первую очередь при сравнении финансовых продуктов.Это базовый процент, который вы будете платить по ссуде или зарабатывать на своем сберегательном счете без учета сложных процентов или комиссий. Это означает, что фактическая сумма процентов, которую вы зарабатываете или платите, скорее всего, будет выше указанной годовой процентной ставки.

Не путать с …

Ставка сравнения

Ставка сравнения, также называемая годовой процентной ставкой, представляет собой «истинную» стоимость ссуды, включая не только процентную ставку, но и любые комиссии и взимаемые сборы.Он разработан, чтобы дать заемщикам более четкое и точное представление о том, сколько им может стоить заем.

Эффективная годовая процентная ставка

Также известная как годовая процентная доходность, это процентное значение, учитывающее эффект сложного процента в течение срока действия вашего кредита или счета. Это число, на которое вы должны смотреть, чтобы лучше понимать, какой интерес вы будете проявлять по месяцам.

Почему важна годовая процентная ставка?

Годовая процентная ставка — это цифра, на которой основаны все остальные ставки, которые вам нужно знать.Это ваша базовая ставка — и хотя это не всегда лучший способ сравнения продуктов разных финансовых институтов, она составляет большую часть того, что вам нужно учитывать.

Вам также понадобится стандартная процентная ставка, если вы планируете рассчитывать проценты по ссуде самостоятельно. Или вы можете использовать наши удобные калькуляторы погашения.

Что еще мне следует учесть?

Процентная ставка — не единственное, что важно учитывать при сравнении банковских продуктов.Вы должны принять во внимание предложение в целом, включая такие факторы, как комиссии, функции и специальные бонусные предложения.

Сборы и сборы

Имея ссуду или счет для хранения сбережений, вам, возможно, придется учитывать дополнительные сборы и сборы, помимо процентов. Для ссуд это может означать регистрационный сбор, ежемесячное обслуживание или годовую плату, в то время как со сберегательного счета может взиматься ежемесячная плата за счет или комиссия за транзакцию.

Вы можете использовать коэффициент сравнения при просмотре ссуд — он учитывает установленные комиссии, которые вы будете платить, или когда вы сравниваете сберегательные или банковские счета, рекомендуется использовать сравнение, подобное Мозо, которое показывает процентная ставка рядом с комиссией по счету.

Компаундирование

В идеальном мире вам нужно учитывать только простой интерес. К сожалению, начисление сложных процентов — важный фактор, который необходимо учитывать, особенно при заимствовании. Эффективная годовая процентная ставка покажет влияние сложного процента на ваши проценты, так что следите за ней.

Ссуды с фиксированным сроком, как и жилищный кредит, рассчитываются таким образом, чтобы каждый ежемесячный платеж был одинаковым, но понимание сложного процента особенно важно для таких вещей, как кредитные карты.Поскольку ваши платежи зависят от ваших расходов и суммы, которую вы решите выплатить, проценты могут увеличиваться каждый месяц по-разному. Посетите нашу страницу процентных ставок по кредитной карте для получения дополнительной информации.

Функции

Процентные ставки не учитывают дополнительные комиссии, которые могут иметь большое значение для того, как вы можете использовать свои деньги. Возможности, которые вы, возможно, захотите рассмотреть, включают в себя онлайн-банкинг или варианты доступа к филиалу, вводные или бонусные периоды процентной ставки или, особенно для кредитов, такие вещи, как компенсационный счет, дополнительные выплаты, каникулы погашения или возможность перерисовки.

Имейте в виду, что некоторые дополнительные функции могут означать дополнительные сборы или изменение вашей процентной ставки, поэтому важно взвесить затраты и выгоды — действительно ли вы будете использовать все функции, за которые платите?

Как сравнить годовые процентные ставки

Перейдите на нашу страницу сравнения процентных ставок бесплатно, легко читаемые сравнения ряда различных банковских продуктов. Вы также можете использовать финансовые калькуляторы Mozo, чтобы узнать, как разные процентные ставки могут повлиять на ваш кредит или счет.

.