Действующая ключевая ставка: Компенсация за задержку выплаты зарплаты
Ключевая ставка — 2021 | Современный предприниматель
Ключевая ставка ЦБ на 2021 год в настоящее время равна 4,25%. Ее значение изменится не ранее следующего заседания Совета директоров Банка России, которое намечено на 19.03.2021 г. Величина этого показателя формируется на основе различных экономических показателей – уровня инфляции, деловой активности населения, условий кредитно-денежной политики, наличия внутренних и внешних рисков для финансового рынка и др.
Ключевая ставка в 2021 году: основания для повышения или понижения ее значения
Регулируя размер ключевой ставки (сокращенно — КС), Центробанк имеет возможность влиять на экономические процессы, происходящие в стране. Теоретически это выражается в следующем:
1. Активизация/замедление экономического роста.
- Понижение КС его ускоряет, так как банки кредитуются у ЦБ под более низкий процент, и соответственно выдают более дешевые кредиты, в том числе, и бизнесу. Например, если ключевая ставка 2021 года составляет 4,25 процента, то такой же является минимальная ставка по кредитам Центробанка. Проценты по вкладам, наоборот, снижаются, людям становится невыгодно копить деньги, они начинают их больше тратить, оживляя экономику.
- Повышение КС дает обратный результат – ставки по вкладам растут, но более дорогими становятся и кредиты, так как под больший процент банки берут их у ЦБ. Население больше сберегает и меньше тратит, меньше берет кредиты. Экономика замедляется – падает спрос на товары, услуги, жилье, турпутевки и проч.
2. Рост/снижение инфляции.
- Если ключевая ставка ЦБ на 2021 год в дальнейшем снизится, это может привести к резкому росту спроса на товары/услуги, а если товаров не будет в достаточном количестве – к инфляции. Деньги легче получить в банке, но они обесцениваются, купить на них можно меньше, чем раньше.
- Если ключевую ставку повысят, деньги станут «дороже», и желание населения поскорее приобрести на них что-либо уменьшится.
 Спрос, а затем и продажи, упадут. И, если рынок конкурентный, упадут и цены, снижая инфляцию.
Спрос, а затем и продажи, упадут. И, если рынок конкурентный, упадут и цены, снижая инфляцию.
3. Курс рубля.
- При снижении КС, как правило, снижается и курс национальной валюты.
- При увеличении КС повышается спрос на рубли, он укрепляется в соотношении к другим валютам.
Опосредованно манипуляции с ключевой ставкой влияют и на уровень безработицы. Ее снижение оживляет производства, и приводит к увеличению спроса на рабочую силу. А непродуманное повышение КС может вызвать всплеск увольнения сотрудников и сокращения рабочих мест.
Февральское заседание по ключевой ставке 2021 года: итоги
По итогам последнего заседания Банк России выпустил пресс-релиз, где обосновал принятое решение о сохранении ключевой ставки на уровне 4,25% (таковой она остается с 27 июля 2020 года). Кроме того, после завершения заседания ЦБ по ключевой ставке 2021 г. с обращением выступила глава Центробанка РФ Эльвира Набиуллина, разъяснившая позицию регулятора.
Из выступления руководителя ЦБ можно сделать вывод, что действующая КС является оптимальной, так как позволяет не «разогнать» инфляцию и пролонгировать выдачу недорогих кредитов, а значит, способствовать развитию производства. Однако именно инфляционные процессы вызывают озабоченность Центробанка. Э. Набиуллина отметила, что они превысили прогнозные ожидания, и только за первый месяц текущего года (ключевая ставка за январь 2021 года тоже составляла 4,25%) инфляция достигла 5,2%.
Поэтому возможно, что несмотря на рекомендации Международного валютного фонда, рекомендовавшего еще больше понизить ключевую ставку, ЦБ выберет другую тактику и, напротив, в недалеком будущем увеличит ее значение.
В пресс-релизе банка России говорится, что одной из причин повышенной инфляции может быть ослабление рубля, падение производства в период коронавирусной пандемии, возросший спрос населения на товары и услуги, который бизнес пока не в состоянии полностью удовлетворить.
Все изменения по ключевой ставке (ставке рефинансирования) с 2018 года вы можете посмотреть здесь.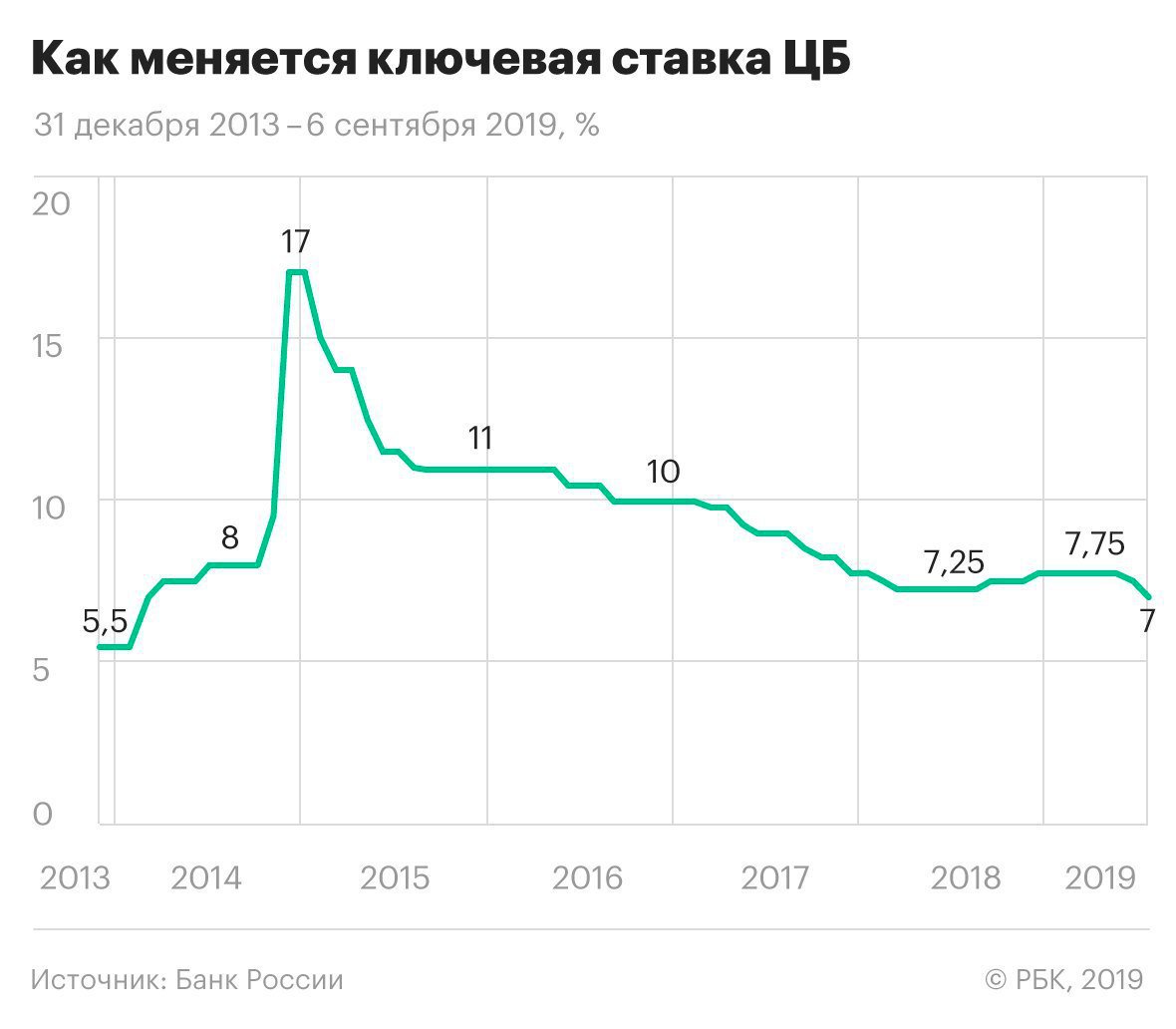
На что еще влияет ключевая ставка ЦБ РФ 2021 года
Значение действующей ключевой ставки применяется при расчете различных штрафных санкций, неустоек. Например, в ст. 395 Гражданского кодекса РФ говорится, что, исходя из ее величины, начисляются проценты на сумму денежного долга, если иной порядок не установлен договором или другим законом. Подобный расчет в т.ч. используется при просрочке очередного погашения кредита, при неправомерном удержании чужих денег, уклонении от их возврата.
С января 2016 года размер ставки рефинансирования приравнивается к значению ключевой ставки ЦБ (Указание Центробанка РФ от 11.12.2015 № 3894-У). Поэтому, применяя нормы закона, где упоминается рефставка, сейчас нужно исходить из действующей ключевой ставки Центробанка. Для примера можно привести ст.75 Налогового кодекса РФ о начислении налоговых пеней, где сказано, что процентная ставка пени для физлиц и ИП принимается равной 1/300 от действующей в период просрочки рефставки, а для организаций – 1/300 от рефставки за первые 30 дней просрочки и 1/150 — за последующие дни просрочки платежа. В данном случае пени исчисляют исходя именно из ключевой ставки Центробанка.
Центробанк разработает порядок изменения ставок по выданным ипотечным кредитам
В Центробанке собираются установить общие правила повышения ипотечной ставки по кредитам, выданным с переменной ставкой. В таком случае в первые годы после выдачи ипотеки действует низкая процентная ставка и заемщики почти ничего не платят по взятому кредиту, а после завершения льготного периода ставка растет. Пока таких программ в линейке предложений банков немного, но они снова начали появляться.
Чтобы заемщики заранее понимали, что будет происходить после завершения льготного периода, сейчас для банков собираются установить общие правила повышения процентных ставок по таким программам.
К числу таких программ относится, например, сельская ипотека. Заемщики берут кредит на покупку или строительство дома за городом по льготной ставке не выше 3% годовых. Но эта ставка может не сохраниться на весь срок кредитования, который по этой программе составляет 25 лет.
Но эта ставка может не сохраниться на весь срок кредитования, который по этой программе составляет 25 лет.
В кредитном договоре заемщика с банком определено, что ставка может быть повышена при несоблюдении условий программы. К таким требованиям относится необходимость прописаться в купленном в ипотеку доме в течение 180 дней с момента его приобретения. Кроме того, ставка по сельской программе может быть повышена, если Минсельхоз не получит средства из бюджета на субсидирование процентов по программе. В таком случае новая ставка будет рассчитываться по формуле: ключевая ставка Центробанка, действующая на момент этих изменений, плюс 2,7%.
В настоящий момент ключевая ставка ЦБ составляет 4,25%. Если бы повышение ставки по сельской ипотеке произошло сейчас, заемщики выплачивали бы взятый кредит по ставке 6,95% годовых.
Смотреть условия сельской ипотеки – 2021
Онлайн-заявка на ипотеку
Получите решение банка в течение 10 минут
ПАО РОСБАНК Генеральная лицензия ЦБ РФ №2272 от 28.01.2015 г.
Банковские вклады становятся все менее выгодными для россиян
СПРАВКА
Андрей Загородний родился в Москве. В 1998 г. окончил РЭА им. Г.В. Плеханова по специальности «финансы и кредит». Работает на фондовом рынке с 1997 г. С 1998 г. – в Банке «ЦентроКредит», с 2012 г. занимает должность заместителя начальника Казначейства.
Банк «ЦентроКредит» основан в 1989 г. Предоставляет клиентам инвестиционные услуги в части операций с российскими и зарубежными ценными бумагами, в том числе торговли еврооблигациями на внебиржевом и биржевом рынках, доступ на валютный рынок и рынок драгоценных металлов, на срочный рынок Московской биржы, доступ к биржевому рынку РЕПО.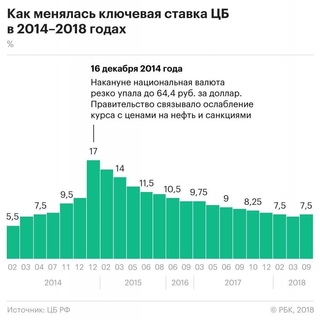
«Остается неопределенность и в отношении санкций, и по части успехов в борьбе с коронавирусом»
– В какой фазе, по-вашему, сейчас находится фондовый рынок?
– Разумеется, на нем сейчас присутствует нестабильность. Вместе с тем есть признаки того, что рынок консолидируется после предыдущей стадии роста. Мы это видим в том числе по нашим клиентам – предновогодний и посленовогодний всплески были использованы ими в основном для фиксации прибыли. На протяжении второй половины 2020 года многие российские инвесторы активно вкладывались в акции компаний-экспортеров, так или иначе связанных со сталью, которые в этот период показали очень неплохой рост. В начале 2021 года они по большей части зафиксировали прибыль. Сейчас на рынке неопределенность, клиенты сидят в кеше и думают, куда вкладываться дальше.
– Неопределенность, потому что люди фиксируют прибыль и непонятно, куда двинутся дальше? Или они фиксируют прибыль, потому что не понимают, что дальше?
– Скорее всего, это взаимосвязано. Произошел неплохой рост, в том числе покупались дивидендные акции, инвесторы искали альтернативы банковским депозитам, ставки по которым падали, ближе к концу года стали искать и альтернативы вложениям в ОФЗ. По части этих дивидендных акций была зафиксирована прибыль, теперь нужно решать, что делать с полученными деньгами.
Подобную ситуацию мы видим не только по российскому рынку, а в целом по всему миру. Причем по России мы видим, что даже на фоне роста нефти, которая показала двухгодичные максимумы, серьезных причин делать ставку на дальнейший рост нет – остается неопределенность и в отношении санкций, и по части успехов в борьбе с коронавирусом.
Интересно при этом, что в целях диверсификации вложений наши клиенты стали довольно часто рассматривать золото – оно лучше всего выполняет роль некой безопасной инвестиции в те моменты, когда инвесторы сильно напуганы или на рынке есть неопределенность. Точно так же золото обычно чувствительно к процентным ставкам: когда они снижаются, падает и доходность облигаций, что, как правило, приводит к достаточно позитивным движениям цен на золото
Точно так же золото обычно чувствительно к процентным ставкам: когда они снижаются, падает и доходность облигаций, что, как правило, приводит к достаточно позитивным движениям цен на золото
– А почему золото? Есть же и другие защитные активы.
– Да, конечно, это качественные дивидендные акции и ОФЗ. Но и те и другие сильно подорожали. Соответственно, пришло время обратить внимание и на золото.
– Как они его покупают? На срочном рынке МосБиржи?
– Нет, срочный рынок, если мы говорим про FORTS МосБиржи, – это больше спекулятивный инструмент. Я же имею в виду покупку непосредственно физического золота на той же Московской бирже, она не так давно запустила этот инструмент, точнее – брокеры не так давно стали делать его доступным для массового розничного инвестора. Он как раз для консервативных инвесторов.
«Интерес к золоту возникает во время всех кризисов, но раньше в России не было ликвидного инструмента»
– Как идут торги и где депонируется это физическое золото?
– Сделки без НДС, торги идут в граммах, цены – в рублях, но они в конечном итоге привязаны к стоимости унции в долларах на лондонской бирже. И консервативные инвесторы покупают золото именно так, потому что фьючерсы – для спекулянтов, там нужно постоянно поддерживать объем гарантийного обеспечения, следить за вариационной маржой, каждые несколько месяцев, после закрытия контракта, покупать новый фьючерс и так далее. А здесь купил – и сиди спокойно. Что касается депонирования, занимается организацией торгов Московская биржа, соответственно, все золото находится на ее счетах.
– То есть это типа металлического счета в банке, но только на брокерском счете?
– В принципе да, но не совсем. Все-таки обезличенный металлический счет не имеет никакой привязки к текущим котировкам. Банки сами выставляют цены покупки и продажи металла. И там достаточно большие спреды. А здесь реальная котировка на Московской бирже, есть возможность покупать и продавать, цена привязана к цене на Лондонской бирже.
– Не проще ли тогда купить золото напрямую на Лондонской бирже? Скажем, через иностранного брокера. И насколько ликвиден этот рынок в России?
– Можно, конечно. Но здесь надо понимать, что в случае каких-то проблем возникают риски юрисдикции – судись потом по месту прописки брокера в каком-нибудь офшоре. Здесь все регулируется Московской биржей, все четко и по реальному курсу. При этом рынок достаточно ликвидный, есть несколько маркетмейкеров, которые поддерживают котировки.
– Чем хороши и чем плохи такие инвестиции в золото? Какие у них характерные риски?
– Если мы говорим про торговлю золотом на Московской бирже, большой плюс в том, что там торговля идет за рубли и у российского инвестора есть возможность купить металл, не теряя средства на конвертации валюты. И это золото можно держать в портфеле как один из активов и использовать для разных целей, как используются обычные ценные бумаги. Например, под его обеспечение можно покупать ценные бумаги и, наоборот, покупать золото под обеспечение ценных бумаг. То есть работать с активами в рамках единого риск-менеджмента, следя лишь за суммарной позицией. Минусов же практически нет, золото – достаточно стабильный защитный актив, серьезных колебаний стоимости по нему нет.
– Вы сказали, что МосБиржа недавно запустила этот контракт. На вашей памяти в предыдущие кризисы к золоту был интерес?
– Да, интерес к золоту так или иначе возникает во время всех кризисов, но раньше в России не было ликвидного инструмента, который позволил бы это золото купить. В основном люди, которые хотели купить золото, открывали металлические счета или покупали монеты, а это все-таки немного не то.
В историческом же плане можно отметить, что золото, как правило, показывает хорошие результаты на фоне откатов фондового рынка и высокой инфляции. Кроме того, за последнее десятилетие золото было более эффективным в плане соответствия динамики цены темпам роста мировой денежной массы, чем казначейские векселя США, тем самым лучше помогая инвесторам сохранять капитал.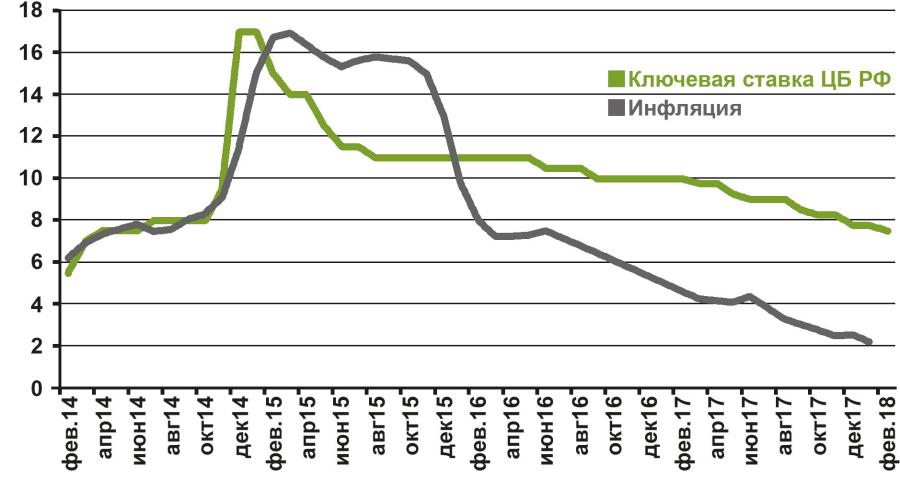
«Есть веские причины, по которым центральные банки продолжат отдавать предпочтение золоту»
– В чем в данном плане особенности текущей ситуации?
– Нынешний кризис – не исключение. Пандемия COVID-19 увеличила неопределенность, усугубляя существующие риски и создавая новые, хотя к концу прошлого года многие инвесторы с оптимизмом считали, что худшее уже позади. Мы полагаем, что инвестиционный спрос на золото будет оставаться устойчивым, в то время как его потребление должно вырасти от начавшегося восстановления экономики, особенно на развивающихся рынках. При этом золото было одним из наиболее прибыльных основных активов 2020 года благодаря сочетанию высокого риска и низких процентных ставок. Золото также имело одну из самых низких просадок в течение года, что помогало инвесторам ограничивать убытки и управлять риском волатильности в своих портфелях.
Кроме того, сейчас многие инвесторы обеспокоены потенциальными рисками, связанными с увеличением бюджетного дефицита, который в сочетании с низкими процентными ставками и ростом денежной массы может привести к инфляционному давлению. Эта озабоченность подчеркивается тем, что центральные банки, в том числе ФРС США и Европейский центральный банк, заявили о большей терпимости к временному превышению уровня инфляции традиционных целевых диапазонов.
– А сами центральные банки сейчас покупают золото или продают?
– Ситуация пока не до конца ясна. В I полугодии прошлого года наблюдался нетто-спрос со стороны центральных банков, их покупки превышали продажи. Во второй половине года спрос стал более изменчивым, колеблясь между ежемесячными чистыми покупками и чистыми продажами. Это было заметное изменение по сравнению с последовательными покупками, наблюдавшимися в течение многих лет, отчасти оно было вызвано решением Банка России приостановить свою программу покупок в апреле. Но мы ожидаем, что в 2021 году покупки будут преобладать – есть веские причины, по которым центральные банки продолжат отдавать предпочтение золоту как части своих валютных резервов, что в сочетании с низкими процентными ставками будет делать драгметалл привлекательным.
– Все-таки золото в основном воспринимается как защитный актив. Какова, по-вашему, вероятность резкой коррекции на фондовом рынке в нынешней ситуации?
– Коррекция, конечно, возможна. Если мы посмотрим на индекс S&P, с точки зрения мультипликатора P/S, то есть отношения стоимости компаний к их выручке, он сейчас находится на рекордных уровнях. Обычно, если этот показатель около единицы, считается, что компания более-менее интересна к покупке. Сейчас он около 3х. Если ориентироваться на данный мультипликатор, очевидно, что риск коррекции достаточно большой. Кроме того, инвесторы, особенно в США, обеспокоены рисками, связанными с увеличением бюджетного дефицита, который в сочетании с низкими процентными ставками может привести к увеличению инфляции.
– При чем тут акции?
– Это все взаимосвязано. Президент США Джо Байден анонсировал помощь американской экономике на сумму порядка 2 триллионов долларов. Инвесторы ждут соответствующих решений, но не стоит ожидать, что данные шаги будут позитивно восприняты рынками. Остаются опасения относительно того, что вливания этих средств в экономику окажутся не особенно эффективными. И если так – это приведет к более раннему сворачиванию сверхмягкой денежно-кредитной политики ФРС и программ помощи экономике.
– Инвесторы опасаются, что при таком сценарии ставки все-таки поднимутся?
– Скорее опасаются того, что инфляция вырастет и просто прекратится стимулирующая политика, закончится рост американской экономики.
– Какие бумаги вы клиентам сейчас советуете покупать?
– Мы достаточно консервативны. Советуем вложения в дивидендные акции и облигации.
Ключевая ставка ЦБ РФ. Досье — Биографии и справки
ТАСС-ДОСЬЕ. Ключевая ставка — годовой процент, под который Банк России (ЦБ РФ) выдает кредиты коммерческим банкам. Решением совета директоров ЦБ РФ 13 сентября 2013 г. ключевой была установлен учетная ставка по аукционам РЕПО (от англ. repurchase agreement, repo; покупкой денег или ценных бумаг с обязательством обратной продажи через определенный срок по фиксированной цене) со сроком 1 неделя. К ключевой привязаны остальные ставки по операциям Банка России, кроме ставки рефинансирования.
repurchase agreement, repo; покупкой денег или ценных бумаг с обязательством обратной продажи через определенный срок по фиксированной цене) со сроком 1 неделя. К ключевой привязаны остальные ставки по операциям Банка России, кроме ставки рефинансирования.
ЦБ РФ может повышать учетную ставку для предотвращения обвального падения рынка и сглаживания биржевых колебаний. При низких учетных ставках банки могут брать рубли в кредит у ЦБ, покупать на них валюту и за счет обесценивания рубля покрывать расходы на выплату процентов по кредиту. При увеличении ставки подобные спекулятивные операции становятся более рискованными для банков. Вместе с тем, рост ставки ведет к удорожанию кредитов для предпринимателей и населения, могут возникнуть трудности с рефинансированием уже выданных кредитов. Это может привести к замедлению темпов экономического роста.
До 2013 г. основной из учетных ставок была ставка рефинансирования. Впервые она была установлена в 1992 г. на уровне 20% годовых, в 1993-1996 гг. достигала уровня в 210%, затем колебалась на уровне 20-50% и после пика 27 мая — 4 июня 1998 г. (150%) постепенно снижалась. Минимальный размер ставки рефинансирования был установлен 1 июня 2010 г. и действовал до 28 февраля 2011 г. — 7,75% Действующая ставка рефинансирования, 8,25%, была установлена 14 сентября 2012 г., однако к началу 2010-х гг. она использовалась только как инструмент по исчислению штрафов, пеней и ориентир для минимального размера процентов по рублевым вкладам населения, а кредиты банкам предоставлялись уже другими инструментами, прежде всего сделками РЕПО.
Впервые минимальная учетная ставка по недельным аукционам РЕПО была установлена ЦБ РФ 20 мая 2003 г. на уровне 6,5% и не менялась вплоть до февраля 2008 г., когда ее повысили на 0,25%. Из-за мирового финансового кризиса и снижения курса рубля в 2008 г. ставка несколько раз повышалась. 1 декабря 2008 г. ее уровень был установлен в 9,5%, а 10 февраля следующего года повышен до 10,5%, вслед за чем последовало укрепление курса рубля. Затем, на протяжении 2009-2010 гг. ставка постепенно снижалась, в частности, уровень в 9,5 годовых был снова зафиксирован 14 мая — 5 июня 2009 г. Исторический минимум ставки по недельным аукционам РЕПО, 5%, держался более полугода — с 1 июня 2010 г. по 28 февраля 2011 г. Уровень в 5,5% годовых был зафиксирован 14 сентября 2012 г., это значение сохранилось после того, как данная ставка была установлена в качестве ключевой.
Затем, на протяжении 2009-2010 гг. ставка постепенно снижалась, в частности, уровень в 9,5 годовых был снова зафиксирован 14 мая — 5 июня 2009 г. Исторический минимум ставки по недельным аукционам РЕПО, 5%, держался более полугода — с 1 июня 2010 г. по 28 февраля 2011 г. Уровень в 5,5% годовых был зафиксирован 14 сентября 2012 г., это значение сохранилось после того, как данная ставка была установлена в качестве ключевой.
Из-за начала конфликта на Украине, ослабления рубля, роста темпов инфляции, введения санкций против российских компаний и других факторов весной — летом 2014 г. ключевая ставка повышалась шесть раз: 1 марта — до 5,5% годовых, 25 апреля — до 7,5%, 25 июля — до 8% годовых, 5 ноября — до 9,5% годовых, 12 и 16 декабря — до 10,5 и 17% соответственно.
МСП Банк снижает ставки по кредитам до 7% годовых
МСП Банк, дочерний банк Корпорации МСП, снизил ставки по кредитам для бизнеса, в том числе для социально-значимых и приоритетных отраслей экономики, до 7% годовых в рамках Программы субсидирования кредитования субъектов МСП Министерства экономического развития РФ.
В начале 2021 года Минэкономразвития РФ внес изменения в программу 1764, согласно которым максимальная конечная ставка для заемщиков определяется как ключевая ставка Банка России (действующая на дату заключения договора), увеличенная на не более чем 2,75%. Как сообщила заместитель министра экономического развития Татьяна Илюшникова, с учетом нынешней ставки Банка России предельная ставка по кредиту составляет 7% годовых.
Льготные ставки будут действовать в рамках всей кредитной линейки банка при соответствии предпринимателей условиям программы Минэкономразвития РФ. Так, малые и средние компании должны соответствовать условиям 209-ФЗ, иметь хорошее финансовое положение и не иметь задолженностей по налогам и зарплате и просроченных платежей по другим кредитам.
Заявку на кредит можно подать дистанционно через систему АИС НГС (smbfin.ru) с помощью электронной подписи. Подробную консультацию можно получить через региональную сеть банка, которая насчитывает 47 центров консультирования предпринимателей по всей России, а также через агентскую сеть банка.
Подробную консультацию можно получить через региональную сеть банка, которая насчитывает 47 центров консультирования предпринимателей по всей России, а также через агентскую сеть банка.
Снижение ставки происходит в рамках участия в реализации национального проекта «Малое и среднее предпринимательство и поддержка предпринимательской инициативы» и направлено на развитие и поддержку малых и средних компаний России.
В кредитной линейке МСП Банка есть специальные кредитные продукты для резидентов ДФО и СКФО, моногородов, высокотехнологичных стартапов и «газелей», а также молодежного и женского предпринимательства. Со списком приоритетных отраслей можно познакомиться на сайте банка: https://mspbank.ru/credit/prioritetnye-nishi/.
Контакты центра консультирования предпринимателей АО «МСП Банк» в г. Улан-Удэ:
670000, Республика Бурятия, г. Улан-Удэ, ул. Смолина, д. 65, телефон: 8 (963) 716 32 40
Банк России принял решение о снижении ключевой ставки до 11 %
31.07.2015
Совет директоров Банка России в пятницу, 31 июля, принял решение снизить ключевую ставку c 11,5% до 11%. Свое решение регулятор объяснил тем, что «баланс рисков по-прежнему смещен в сторону существенного охлаждения экономики».
Регулятор будет принимать решения по ставке в зависимости от изменения баланса инфляционных рисков и рисков охлаждения экономики.
Снижение ставки стало пятым подряд за год, сообщается в пресс-релизе регулятора.
ЦБ объясняет свое решение тем, что баланс рисков по-прежнему смещен в сторону существенного охлаждения экономики, несмотря на некоторое увеличение инфляционных рисков.
Следующее заседание ЦБ пройдет 11 сентября.
Решение ЦБ совпало с ожиданиями экспертов. Опрошенные ТАСС накануне собрания аналитики в основном полагали, что регулятор снизит ключевую на 0,5 п.п. 10 экспертов из 15 ожидали, что с прежних темпов снижения ставки в 1-2 п. п. регулятор замедлится до 0,5 п.п. При этом еще пять считали, что ЦБ в этот раз возьмет паузу и, таким образом, прервет последовательное снижение ставки, которая в этом году опускалась уже четыре раза — с 17% до 11,5%.
п. регулятор замедлится до 0,5 п.п. При этом еще пять считали, что ЦБ в этот раз возьмет паузу и, таким образом, прервет последовательное снижение ставки, которая в этом году опускалась уже четыре раза — с 17% до 11,5%.
В ЦБ также отметили, что прогнозируют значительное замедление годовой инфляции в начале 2016 года, в том числе из-за высокой базы 2015 года, в частности, прогнозируется снижение инфляции до уровня менее 7% в июле 2016 года.
По оценкам регулятора, по состоянию на 27 июля годовой темп прироста потребительских цен составил 15,8% после 15,3% в июне. Темпы инфляции выросли, прежде всего, за счет повышения тарифов естественных монополий в начале текущего месяца.
Кроме того, Банк России может ухудшить прогноз по снижению ВВП РФ в 2015 году из-за более значительного, чем ожидалось, сокращения внутреннего спроса в первом полугодии 2015 года.
По оценкам ЦБ, снижение ВВП во втором квартале к соответствующему периоду прошлого года было более существенным, чем в первом квартале.
Как менялась ключевая ставка Банка России. Досье
ТАСС-ДОСЬЕ. Ключевая ставка — годовой процент, под который Банк России (ЦБ РФ) выдает кредиты коммерческим банкам. Решением совета директоров ЦБ РФ 13 сентября 2013 г. ключевой была установлена учетная ставка по аукционам РЕПО (от англ. repurchase agreement, repo; покупка денег или ценных бумаг с обязательством обратной продажи через определенный срок по фиксированной цене) со сроком 1 неделя. К ключевой привязаны остальные ставки по операциям Банка России, кроме ставки рефинансирования.
ЦБ РФ может повышать учетную ставку для предотвращения обвального падения рынка и сглаживания биржевых колебаний. При низких учетных ставках банки могут брать рубли в кредит у ЦБ, покупать на них валюту и за счет обесценивания российской валюты покрывать расходы на выплату процентов по рублевым кредитам. При увеличении ставки подобные спекулятивные операции становятся более рискованными для банков.%20(1).png) Вместе с тем, рост ставки ведет к удорожанию кредитов для предпринимателей и населения, у банков могут возникнуть трудности с рефинансированием уже выданных кредитов. Это может привести к замедлению темпов экономического роста.
Вместе с тем, рост ставки ведет к удорожанию кредитов для предпринимателей и населения, у банков могут возникнуть трудности с рефинансированием уже выданных кредитов. Это может привести к замедлению темпов экономического роста.
До 2013 г. основной из учетных ставок была ставка рефинансирования. Впервые она была установлена в 1992 г. на уровне 20% годовых, в 1993-1996 гг. доходила до 210%, затем колебалась на уровне 20-50% и после пика 27 мая — 4 июня 1998 г. (150%) постепенно снижалась. Минимальный размер ставки рефинансирования был установлен 1 июня 2010 г. и действовал до 28 февраля 2011 г. — 7,75% Действующая ставка рефинансирования, 8,25%, была установлена 14 сентября 2012 г., однако к началу 2010-х гг. она использовалась только как инструмент по исчислению штрафов, пеней, а также в качестве ориентира для минимального размера процентов по рублевым вкладам населения. Кредиты банкам предоставлялись уже с помощью других инструментов, прежде всего сделками РЕПО.
Впервые минимальная учетная ставка по недельным аукционам РЕПО была установлена ЦБ РФ 20 мая 2003 г. на уровне 6,5% и не менялась вплоть до февраля 2008 г., когда ее повысили на 0,25% Из-за мирового финансового кризиса и снижения курса рубля в 2008 г. ставка несколько раз повышалась. 1 декабря 2008 г. ее уровень был установлен в 9,5%, а 10 февраля следующего года поднят до 10,5%, вслед за чем последовало укрепление курса рубля. Затем, на протяжении 2009-2010 гг. ставка постепенно снижалась, в частности, уровень в 9,5% годовых был снова зафиксирован 14 мая — 5 июня 2009 г. Исторический минимум ставки по недельным аукционам РЕПО, 5%, держался более полугода — с 1 июня 2010 г. по 28 февраля 2011 г. Уровень в 5,5% годовых был зафиксирован 14 сентября 2012 г., это значение сохранилось после того, как данная ставка была установлена в качестве ключевой.
Из-за начала конфликта на Украине, ослабления рубля, роста темпов инфляции, введения санкций против российских компаний и других факторов весной — летом 2014 г. ЦБ повышал ключевую ставку шесть раз: 1 марта — до 5,5% годовых, 25 апреля — до 7,5%, 25 июля — до 8% годовых, 5 ноября — до 9,5% годовых, 12 и 16 декабря — до 10,5 и 17% соответственно.
ЦБ повышал ключевую ставку шесть раз: 1 марта — до 5,5% годовых, 25 апреля — до 7,5%, 25 июля — до 8% годовых, 5 ноября — до 9,5% годовых, 12 и 16 декабря — до 10,5 и 17% соответственно.
Но уже 30 января 2015 г. ЦБ РФ снизил ключевую ставку до 15%, объяснив это тем, что предыдущий подъем привел к стабилизации инфляционных и девальвационных ожиданий. Финансовый регулятор ожидал уменьшения инфляции в среднесрочной перспективе. 13 марта 2015 г. ключевая ставка была снижена до 14% годовых, 30 апреля — до 12,5% годовых, 15 июня — до 11,5% годовых. При этом в июне 2015 г. Банк России заявил, что готов продолжить снижение ключевой ставки по мере дальнейшего замедления роста потребительских цен.
Количество просмотров — 1197
Расскажи друзьям о том, что ищешь недвижимость и подари им интересную ссылку!
МСП Банк снижает ставки по кредитам до 7% годовых
МСП Банк 25 января 2021 14:59
МСП Банк, дочерний банк Корпорации МСП, снизил ставки по кредитам субъектам , в том числе для социально-значимых и приоритетных отраслей экономики, до 7% годовых в рамках Программы субсидирования кредитования субъектов МСП Министерства экономического развития РФ.
В начале 2021 года Минэкономразвития РФ внес изменения в программу 1764, согласно которым максимальная конечная ставка для заемщиков определяется как ключевая ставка Банка России (действующая на дату заключения договора), увеличенная на не более чем 2,75%. Как сообщила заместитель министра экономического развития Татьяна Илюшникова, с учетом нынешней ставки Банка России предельная ставка по кредиту составляет 7% годовых.
Льготные ставки будут действовать в рамках всей кредитной линейки банка при соответствии предпринимателей условиям программы Минэкономразвития РФ. Так, малые и средние компании должны соответствовать условиям 209-ФЗ, иметь хорошее финансовое положение и не иметь задолженностей по налогам и зарплате и просроченных платежей по другим кредитам.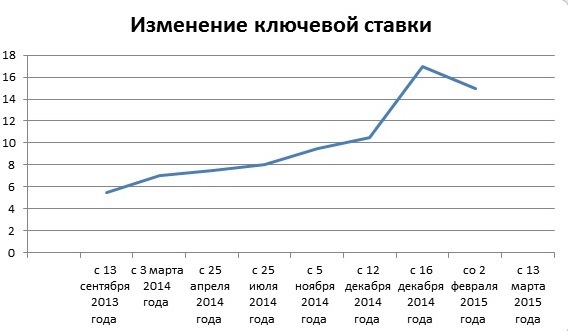
Заявку на кредит можно подать дистанционно через систему АИС НГС (smbfin.ru) с помощью электронной подписи. Подробную консультацию можно получить через региональную сеть банка, которая насчитывает 47 центров консультирования предпринимателей по всей России, а также через агентскую сеть банка.
Снижение ставки происходит в рамках участия в реализации национального проекта «Малое и среднее предпринимательство и поддержка предпринимательской инициативы» и направлено на развитие и поддержку малых и средних компаний России.
В кредитной линейке МСП Банка есть специальные кредитные продукты для резидентов ДФО и СКФО, моногородов, высокотехнологичных стартапов и «газелей», а также молодежного и женского предпринимательства. Со списком приоритетных отраслей можно познакомиться на сайте банка: https://mspbank.ru/credit/prioritetnye-nishi/.
Пресс-релиз подготовлен на основании материала, предоставленного организацией. Информационное агентство AK&M не несет ответственности за содержание пресс-релиза, правовые и иные последствия его опубликования. Длительность ключевой ставки
| Справка по финансовому экзамену 123
При вычислении модифицированной (или эффективной) дюрации для портфеля ценных бумаг мы изменяем процентную ставку номинальной (доходность к погашению) на каждые срока погашения на небольшую величину вверх или вниз (± Δ г). ), и определить процентное изменение цены в портфеле при изменении доходности на 1%. По сути, мы добавляем ± Δ y ко всей кривой номинала. (Посмотрите здесь, чтобы освежить в памяти номинальную кривую, а также узнать, как перенастроить спотовую кривую с номинальной кривой, что мы сделаем чуть позже.) Параллельные сдвиги номинальной кривой выглядят так:
Модифицированная (или эффективная) дюрация полезна для определения того, как изменится цена ценной бумаги или портфеля ценных бумаг, когда кривая (номинальной) доходности претерпевает параллельный сдвиг, но менее полезна (т.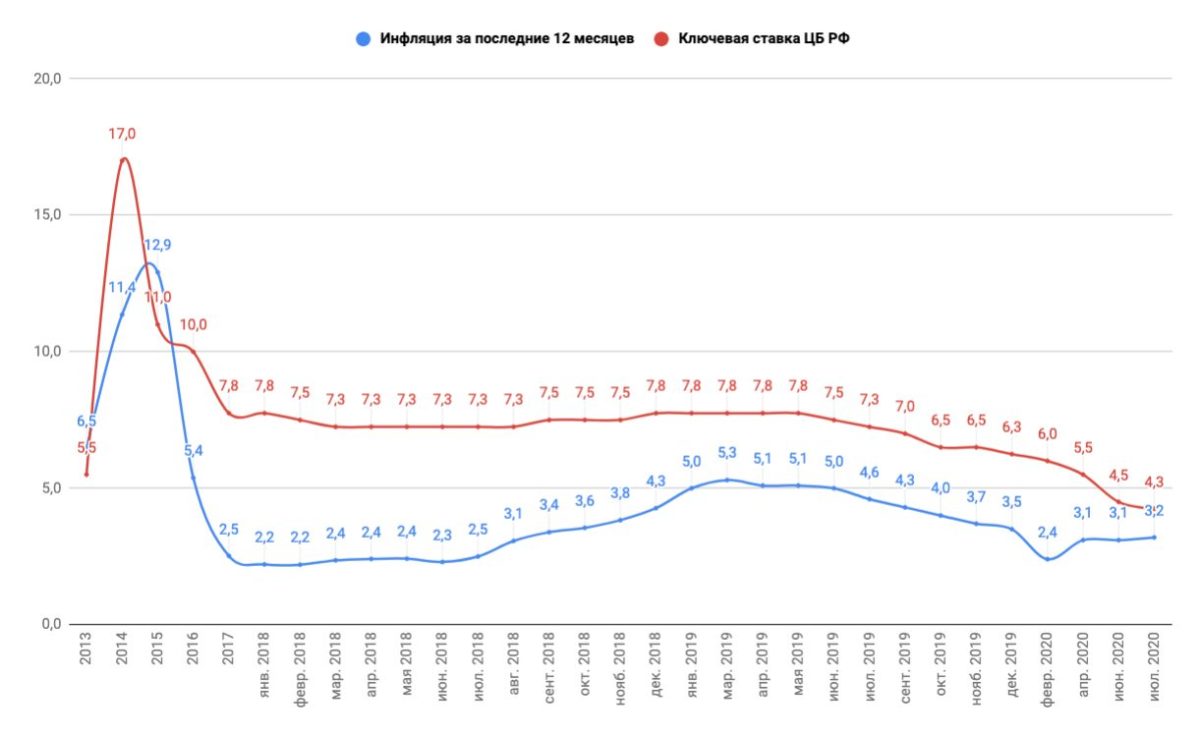 Е. вообще не используется ) когда кривая доходности изменяется не параллельным смещением (например, сглаживание или повышение крутизны). В таких случаях требуется более универсальный способ измерения продолжительности; длительность ключевой ставки как раз такая мера.
Е. вообще не используется ) когда кривая доходности изменяется не параллельным смещением (например, сглаживание или повышение крутизны). В таких случаях требуется более универсальный способ измерения продолжительности; длительность ключевой ставки как раз такая мера.
Идея длительности ключевой ставки (также известной как частичная длительность ) заключается в том, что мы не добавляем ± Δ y ко всей кривой номинала; мы добавляем ± Δ y только к доходности к погашению с определенным сроком погашения на кривой номинала, оставляя без изменений доходность к погашению для всех остальных сроков погашения; этот конкретный срок погашения называется ключевой ставкой . Таким образом, имеем:
- Дюрация ключевой ставки на ½ года: ± Δ y прибавляется к доходности ½ года, в то время как доходность к погашению для всех остальных сроков остается неизменной
- Дюрация двухлетней ключевой ставки: ± Δ г прибавляется к 2-летней доходности к погашению
- Дюрация 5-летней ключевой ставки: ± Δ г добавлено к 5-летней доходности к погашению
- Дюрация 10-летней ключевой ставки: ± Δ y добавлено к 10-летней доходности к погашению
- Дюрация ключевой ставки на 20 лет: ± Δ y добавлено к 20-летней доходности к погашению
- Дюрация 30-летней ключевой ставки: ± Δ г добавлено к 30-летней доходности к погашению
- И так далее
Сдвиги кривой номинальной стоимости для расчета дюрации ключевой ставки выглядят следующим образом:
Обратите внимание, что продолжительность ключевой ставки может быть модифицированной (при условии отсутствия изменений денежных потоков при изменении ключевой ставки) или эффективной (допуская, что денежные потоки могут измениться при изменении ключевой ставки). {\ infty} \ Dur_ {key \ rate_i}
{\ infty} \ Dur_ {key \ rate_i}
\ end {align}
Обратите внимание, что это не бесконечная сумма: в конечном итоге индекс i превысит срок погашения ценной бумаги или портфеля; после этого все дюрации ключевых ставок будут равны нулю (потому что, как мы увидим, все номинальные ставки и все спотовые ставки со сроками погашения короче, чем срок погашения ключевой ставки, не изменятся).
Необычное поведение
Вспоминая связь между кривой номинала и кривой спот, мы можем определить влияние изменений ключевой ставки на облигации с разными сроками погашения и с различными купонами. Чтобы проиллюстрировать эти эффекты, я буду использовать простой пример: плоская кривая доходности 4% с годовыми (эффективными) ставками от 1 года до 10 лет:
| Срок погашения (лет) | Номинальная доходность | Доходность спот |
| 1.0 | 4,0% | 4,0% |
| 2,0 | 4,0% | 4,0% |
| 3,0 | 4,0% | 4,0% |
| 4,0 | 4,0% | 4,0% |
| 5,0 | 4,0% | 4,0% |
| 6,0 | 4,0% | 4,0% |
| 7,0 | 4,0% | 4,0% |
| 8,0 | 4.0% | 4,0% |
| 9,0 | 4,0% | 4,0% |
| 10,0 | 4,0% | 4,0% |
Предположим, мы хотим вычислить 5-летнюю дюрацию ключевой ставки для облигации. Для этого мы добавляем 50 базисных пунктов к 5-летней номинальной ставке (оставляя все остальные номинальные ставки без изменений) и вычисляем влияние на спотовые ставки, затем вычитаем 50 базисных пунктов из 5-летней номинальной ставки (опять же, оставляя все другие номинальные ставки без изменений) и рассчитайте влияние на спотовые ставки. Затем мы будем использовать эти модифицированные спотовые ставки для вычисления \ (P _- \) и \ (P _ + \), а затем использовать их в формуле дюрации.
Затем мы будем использовать эти модифицированные спотовые ставки для вычисления \ (P _- \) и \ (P _ + \), а затем использовать их в формуле дюрации.
Начнем с добавления 50 базисных пунктов к 5-летней номинальной ставке.
Годовая спотовая доходность проста: она остается 4,0%. (Напомним, что однопериодная номинальная ставка и однопериодная спотовая ставка равны, и что годовая номинальная ставка не изменилась; изменилась только пятилетняя номинальная ставка.)
Двухлетняя спотовая доходность также проста: она тоже остается 4.0%, потому что двухлетняя спотовая доходность не изменилась, а годовая спотовая доходность не изменилась.2 \ & = \ \ frac {1040.00} {$ 961.54} \ = \ 1.0816 \\
\\
1 \ + \ s_2 \ & = \ \ sqrt {1.0816} \ = \ 1.0400 \\
\\
s_2 \ & = \ 4.0 \%
\ end {align}
3-летняя спотовая ставка и 4-летняя спотовая ставка также просты: они по-прежнему составляют 4,0%, потому что их номинальная доходность не изменилась, как и все спотовые доходности для более коротких сроков погашения. Я оставлю алгебру тебе.
В качестве захватывающего (! ) изменения темпа 5-летняя спотовая ставка не равна 4,0% (напомним, что мы прибавили 50 базисных пунктов к 5-летней ставке по номинальной ).{1/5} \ = \ 1.045476 \\
\\
s_5 \ & = \ 4.5476 \%
\ end {align}
Этот результат кажется разумным: доходность к погашению составляет 4,5%, поэтому мы получим номинал (1000 долларов США), если дисконтируем всех денежных потоков по ставке 4,5%. Поскольку мы установили скидку на первые четыре платежа на уровне 4% (менее 4,5%), мы должны дисконтировать окончательный платеж на уровне более 4,5%, чтобы в среднем получить скидку 4,5% на все. А поскольку первые четыре платежа намного меньше окончательного платежа, разница в окончательной ставке дисконтирования должна быть намного меньше, чем разница (50 б. п.) по первым четырем: она равна 4.{1/6} \ = \ 1.039820 \\
п.) по первым четырем: она равна 4.{1/6} \ = \ 1.039820 \\
\\
s_6 \ & = \ 3.9820 \%
\ end {align}
Опять же, этот результат имеет смысл: 5-летняя спотовая ставка увеличилась, поэтому единственный способ сохранить неизменной 6-летнюю номинальную ставку — это понизить 6-летнюю спотовую ставку. И, опять же, поскольку окончательный платеж намного превышает первые 5 (только купонных) выплат, снижение должно быть небольшим по сравнению с увеличением 5-летней спотовой ставки: 5-летняя спотовая ставка на 54,76 б.п. выше, чем доходность к погашению — 4%, а 6-летняя спотовая ставка — 1.На 80 б.п. ниже доходности к погашению.
Обратите внимание, как изменение 5-летней ключевой ставки приводит к некоторым неожиданным результатам. Например, 6-летняя бескупонная облигация будет иметь цену немного выше на (поскольку 6-летняя спотовая ставка на ниже ), когда 5-летняя ключевая ставка увеличена ; Другими словами, 6-летняя бескупонная облигация будет иметь отрицательную 5-летнюю дюрацию ключевой ставки . (Помните, что при повышении процентных ставок цены на облигации обычно снижаются, и эта дюрация обычно положительна.Когда цена увеличивается с увеличением ставки, продолжительность должна быть отрицательной.)
Продолжая в той же утомительной манере, получаем:
| Срок погашения (лет) | Номинальная доходность | Доходность спот |
| 1,0 | 4,0000% | 4,0000% |
| 2,0 | 4,0000% | 4,0000% |
| 3,0 | 4,0000% | 4.0000% |
| 4,0 | 4,0000% | 4,0000% |
| 5,0 | 4,5000% | 4,5476% |
| 6,0 | 4,0000% | 3,98 20% |
| 7,0 | 4,0000% | 3,9846% |
| 8,0 | 4,0000% | 3,98 65% |
| 9,0 | 4,0000% | 3. 9880% 9880% |
| 10,0 | 4.0000% | 3.9892% |
Графически:
Если вычесть 50 б.п. из 5-летней номинальной ставки, мы получим:
| Срок погашения (лет) | Номинальная доходность | Доходность спот |
| 1,0 | 4,0000% | 4,0000% |
| 2,0 | 4,0000% | 4,0000% |
| 3,0 | 4.0000% | 4,0000% |
| 4,0 | 4,0000% | 4,0000% |
| 5,0 | 3,5000% | 3,4641% |
| 6,0 | 4,0000% | 4,0 182% |
| 7,0 | 4,0000% | 4.0156% |
| 8,0 | 4,0000% | 4,0136% |
| 9,0 | 4,0000% | 4,0121% |
| 10.0 | 4,0000% | 4.0109% |
Графически:
Срок действия различных облигаций по ключевой ставке
Дюрация ключевой ставки не только зависит от срока погашения облигации (по сравнению со сроком погашения ключевой ставки), но также зависит от купонной ставки облигации по сравнению с ее доходностью к погашению; то есть это зависит от того, оценивается ли облигация по номиналу, с премией или с дисконтом. Используя нашу 4% плоскую кривую доходности, вот дюрации ключевой ставки для пяти 5-летних безопционных облигаций с различными купонными ставками, а также сумма их дюрации ключевой ставки и их эффективная дюрация:
| Срок действия ключевой ставки (лет), 5-летняя облигация | |||||
| Срок погашения по ключевой ставке | Ставка купона | ||||
0. 0% 0% | 2,0% | 4,0% | 6,0% | 8,0% | |
| 1 год | (0,0385) | (0,0174) | 0,0000 | 0,0145 | 0,0268 |
| 2 года | (0,0785) | (0,0354) | 0,0000 | 0,0296 | 0,0547 |
| 3 года | (0.1201) | (0,0542) | 0,0000 | 0,0453 | 0,0838 |
| 4 года | (0,1633) | (0,0737) | 0,0000 | 0,0616 | 0,1140 |
| 5 лет | 5.2081 | 4,7931 | 4,4519 | 4,1666 | 3,9243 |
| 6+ лет | 0,0000 | 0,0000 | 0.0000 | 0,0000 | 0,0000 |
| Сумма | 4.8078 | 4.6125 | 4,4519 | 4,3176 | 4.2036 |
| Dur Eff | 4,8078 | 4,6125 | 4,4519 | 4,3176 | 4,2036 |
Так, например, 5-летняя бескупонная облигация имеет 4-летнюю дюрацию ключевой ставки −0.1633 года; если 4-летняя номинальная ставка увеличится на на 1%, цена облигации на увеличится на примерно на 0,1633%. Пятилетняя облигация с 8% купоном имеет трехлетнюю дюрацию по ключевой ставке 0,0838 года; если трехлетняя номинальная ставка уменьшится на на 1%, цена облигации на увеличится примерно на 0,0838%.
Ключевые идеи, которые можно почерпнуть из этой таблицы:
- Облигации номиналом имеют дюрацию ключевой ставки нулевых лет для любого срока погашения ключевой ставки короче , чем срок погашения облигации
- Дисконт облигаций имеют отрицательные дюрации ключевой ставки для погашения ключевой ставки короче , чем срок погашения облигации; в частности, бескупонных облигаций имеют отрицательных дюрации ключевой ставки для погашения ключевой ставки короче на , чем срок погашения облигации
- Облигации с премией имеют положительных дюрации ключевой ставки для погашения ключевой ставки короче на , чем срок погашения облигации
- Все облигаций имеют дюрацию ключевой ставки нулевых лет для любого срока погашения ключевой ставки длиннее , чем срок погашения облигации
- Сумма дюрации ключевой ставки для всех сроков погашения равна эффективной дюрации облигации
Обратите внимание, что эти последние два пункта уже были рассмотрены в разделе «Ожидаемое поведение» выше.
Использование длительностей ключевой ставки
Дюрация ключевой ставки используется для определения влияния непараллельных сдвигов кривой доходности на портфель облигаций. (Фактически, их также можно использовать для определения эффекта параллельных сдвигов кривой доходности, хотя они менее эффективны, чем простое использование эффективной дюрации каждой облигации.) Например, предположим, что у нас есть эта кривая номинальной доходности:
Предположим, что мы ожидаем, что кривая доходности выровняется: рост на 50 базисных пунктов на коротком конце, падение на 50 базисных пунктов на длинном конце, с линейным переходом между ними:
| Годы | Сплющивание ∆, т. П. |
| 1.0 | 50,0 |
| 2,0 | 38,9 |
| 3,0 | 27,8 |
| 4,0 | 16,7 |
| 5,0 | 5,6 |
| 6,0 | −5,6 |
| 7,0 | −16,7 |
| 8,0 | −27,8 |
| 9,0 | −38,9 |
| 10,0 | −50,0 |
Новая кривая доходности (по номиналу) будет выглядеть следующим образом:
Чтобы определить влияние этого выравнивания на стоимость портфеля с фиксированной доходностью, мы можем взглянуть на дюрации ключевой ставки каждой облигации в портфеле, умножить дюрацию каждой ключевой ставки на изменение доходности (из таблицы выше) и рыночной стоимости облигации, а затем сложите их.Обратите внимание, что эффективная дюрация (портфеля) здесь не поможет, поскольку сдвиг не является параллельным.
Точно так же, если мы ожидаем, что кривая номинала будет крутым, или горбичным, или сделает что-нибудь еще, кроме параллельного сдвига, дюрации ключевой ставки позволят нам определить влияние первого порядка на стоимость портфеля облигаций с диапазоном сроки погашения.
Как бы то ни было, существует также идея выпуклостей ключевых ставок. Я никогда не слышал о них — я просто сам придумал эту идею, — но для больших изменений урожайности имеет смысл учитывать выпуклость в дополнение к продолжительности.В глубине души я первопроходец.
Заблуждения относительно продолжительности ключевой ставки
Основное заблуждение относительно продолжительности ключевой ставки состоит в том, что она соответствует изменению единой спотовой ставки , а не изменению единой номинальной ставки . Для ясности:
- Дюрация ключевой ставки данной облигации для данного срока погашения — это отношение процентного изменения цены этой облигации к изменению ставки номинальной стоимости при этом сроке погашения , когда , номинальной ставки для всех остальных Срок погашения не изменился .
- Когда номинальная ставка при данном сроке погашения изменяется, а номинальная ставка при всех остальных сроках погашения остается неизменной:
- Спот-ставки со сроками погашения меньше , чем данный срок погашения , не изменятся
- Спот-курс при данный срок погашения изменится на в том же направлении , что и изменение номинального курса, и на сумму больше , чем изменение номинального курса
- Спот-ставки со сроками погашения больше , чем заданный срок погашения, изменятся на в направлении, противоположном изменения номинального курса, и на сумму (намного) меньше , чем изменение номинального курса (и при более длительных сроках погашения изменение будет меньше)
Длительность ключевой ставки по облигациям (KRD) в Excel: расчет и понимание
Все вы знакомы с концепцией облигации Duration , которая сообщает нам, насколько изменится цена облигации, если ее доходность повысится или снизится на небольшую величину.
Несмотря на то, что существует несколько различных определений продолжительности , которые дают несколько разные результаты, одно, которое наиболее близко связано с продолжительностью ключевой скорости , — это модифицированная продолжительность D , которая может быть определена в очень общем виде. по отношению к любому потоку будущих денежных потоков как отрицательное относительное изменение — ΔB / B начальной грязной цены облигации B , вызванное изменением Δy в ее начальной доходности y , деленное на это изменение Δy .В математических терминах:
D = (- ΔB / B) / Δy = — (1 / B) ΔB / Δy
. до еще не установленного размера предполагаемого изменения доходности Δy . Многие отраслевые практики устанавливают Δy = 1% . Например, они сместили бы начальную доходность с y = 5% на y ΄ = y + Δy = 5% + 1% = 6% , а затем рассчитали бы теоретическую цену облигации B ΄ подразумевается смещенной доходностью ΄ .Наконец, они вычислили бы разницу ΔB = B B-B , а затем Duration D по приведенной выше формуле.
Фактическая практика следует несколько иному толкованию приведенной выше формулы, так что как повышение, так и снижение доходности рассматриваются симметрично. Более конкретно, большинство практиков принимают Δy в приведенной выше формуле, чтобы обозначить разницу y + -y — = 2 δ , где y + = y + δ и y — = y- δ и δ — это абсолютный односторонний сдвиг доходности, обычно 1% .Затем они формируют разницу цен грязных облигаций ΔB = B + -B — и подставляют все в формулу, чтобы получить:
Более конкретно, большинство практиков принимают Δy в приведенной выше формуле, чтобы обозначить разницу y + -y — = 2 δ , где y + = y + δ и y — = y- δ и δ — это абсолютный односторонний сдвиг доходности, обычно 1% .Затем они формируют разницу цен грязных облигаций ΔB = B + -B — и подставляют все в формулу, чтобы получить:
D = — (1 / 2B) ΔB / δ
Бесплатная версия с открытым исходным кодом QuantLib вычисляет Модифицированную продолжительность облигаций с фиксированной ставкой аналитически, задав Δy -> 0 , что преобразует формулу определения в формулу, включающую производную дБ / dy из B относительно y :
D = — (1 / B) dB / dy
Затем вместо вычисления теоретических цен облигаций, соответствующих смещенной доходности, QuantLib рассматривает B как сумму B 1 + B 2 +… B n текущей стоимости денежных потоков по облигации B 1 , B 2 ,…, B n . Так как производная действует линейно на сумму, то получается:
Так как производная действует линейно на сумму, то получается:
дБ / dy = дБ 1 / dy + дБ 2 / dy +… + 06 дБ / dy
Теперь каждую производную можно легко вычислить, если мы знаем, как определяется доходность y . Например, если y определено с использованием правила непрерывного сложения , то связанный с ним коэффициент дисконтирования , который применяется к i th денежному потоку C i выплачено в момент T i должен равняться e -yTi , что означает, что Bi = e -yTi C i и, следовательно:
дБ i / dy =
5 d ( -yTi C i ) / dy = -C i T i e -yTi
Преимущество этого подхода заключается в том, что для расчета симметричного двусторонняя производная, необходимая по определению Modified Duration .
Определение и рациональное определение продолжительности ключевой ставки
Теперь, когда мы обновили нашу память деталями модифицированной продолжительности , мы заметили, что текущие значения всех денежных потоков пересчитываются на основе двух крайне нереалистичных предположений:
Допущение 1: Применимо для дисконтирования каждого денежного потока C i — та же фиксированная доходность y , независимо от времени T i , на которое выплачивается C i . Обратите внимание, что и — это чисто теоретическая процентная ставка, связанная с нашей конкретной облигацией (потоком денежных средств), определенная так, что совокупная приведенная стоимость всех денежных потоков равна наблюдаемой грязной цене наблюдаемой облигации. Уберите облигацию, и вы обнаружите, что y не имеют реальной связи с каждым сроком погашения T i отдельно! Единственное значение y состоит в том, что он хорошо выполняет свою работу по отношению к связанной облигации, а именно рассчитывает приведенную стоимость облигации.Помимо этого, соотношение и не может быть применено к какой-либо другой облигации, даже для вычисления приведенной стоимости одного изолированного денежного потока той же облигации.
Обратите внимание, что и — это чисто теоретическая процентная ставка, связанная с нашей конкретной облигацией (потоком денежных средств), определенная так, что совокупная приведенная стоимость всех денежных потоков равна наблюдаемой грязной цене наблюдаемой облигации. Уберите облигацию, и вы обнаружите, что y не имеют реальной связи с каждым сроком погашения T i отдельно! Единственное значение y состоит в том, что он хорошо выполняет свою работу по отношению к связанной облигации, а именно рассчитывает приведенную стоимость облигации.Помимо этого, соотношение и не может быть применено к какой-либо другой облигации, даже для вычисления приведенной стоимости одного изолированного денежного потока той же облигации.
Допущение 2: Новая цена облигации рассчитывается исходя из предположения, что теоретическая фиксированная доходность y , применимая к каждому денежному потоку C i изменяется на ту же величину Δy (дискретная или бесконечно малая), независимо от того времени T i .
Хотя, как уже объяснялось, первое предположение, возможно, нереалистично, но неплохо, поскольку оно по-прежнему дает правильную текущую цену облигации, второе предположение практически полезно только в том случае, если мы заинтересованы в вычислении чувствительности цены облигации к изменению. собственной доходности.Довольно часто нас интересует, как цена облигации реагирует на изменение цены определенных эталонных высоколиквидных облигаций, таких как казначейские облигации, с различным сроком погашения.
Это факт, что цена облигаций меняется по всему спектру сроков погашения. Определенные рыночные события могут привести к скачку краткосрочных процентных ставок или кредитных спредов (оба имеют отношение к доходности облигации), но не повлекут за собой изменений долгосрочных ставок и спредов. Нам нужен не единичный показатель того, насколько чувствительна наша облигация к изменениям общей доходности, а несколько различных показателей, которые количественно определяют чувствительность нашей облигации к различным режимам погашения.Например, мы, возможно, хотели бы иметь три разных чувствительности: a) к изменениям краткосрочных ставок, b) к изменениям среднесрочных ставок и c) к изменениям долгосрочных ставок.
Определенные рыночные события могут привести к скачку краткосрочных процентных ставок или кредитных спредов (оба имеют отношение к доходности облигации), но не повлекут за собой изменений долгосрочных ставок и спредов. Нам нужен не единичный показатель того, насколько чувствительна наша облигация к изменениям общей доходности, а несколько различных показателей, которые количественно определяют чувствительность нашей облигации к различным режимам погашения.Например, мы, возможно, хотели бы иметь три разных чувствительности: a) к изменениям краткосрочных ставок, b) к изменениям среднесрочных ставок и c) к изменениям долгосрочных ставок.
Длительности ключевой ставки ( KRD ) были придуманы именно для этой цели.
Более конкретно, продолжительность ключевой ставки K i определяется по отношению к заданному сроку погашения T i и абсолютному одностороннему сдвигу ставки δ следующим образом:
K i = (B — -B + ) / (2B δ)
Здесь B — — приведенная стоимость облигации (грязная цена), рассчитанная по кривой доходности с нисходящим скачком YC — описан ниже.
B + — приведенная стоимость облигации (грязная цена), рассчитанная по восходящей кривой доходности YC + , также описанной ниже.
Приведенное выше определение основывается на базовой кривой доходности YC , которая точно воспроизводит текущую наблюдаемую цену грязных облигаций B .
Эта базовая кривая доходности YC построена с использованием в качестве исходных рыночных ставок, N непрерывно составных нулевых ставок z 1 , z 2 ,…, z N все равно известному текущему — также непрерывно сложный — доходность облигации y .Как целое число N , так и сроки погашения входных нулевых ставок могут быть выбраны произвольно. Например, мы можем выбрать сроки погашения N = 11 вдоль кривой спот-ставки Казначейства США.
На основании фактов a) кривая доходности YC была построена на основе доходности облигации y и b) доходность облигации y по своему собственному определению дает текущую наблюдаемую грязную цену облигации B , из этого следует, что оценка облигации с использованием коэффициентов дисконтирования YC должна привести к результату, точно равному B .
После того, как мы построили YC , мы строим кривую доходности YC — , просто увеличивая начальную нулевую ставку i th z i вниз на заданную величину δ , при сохранении всех остальных входных скоростей фиксированными.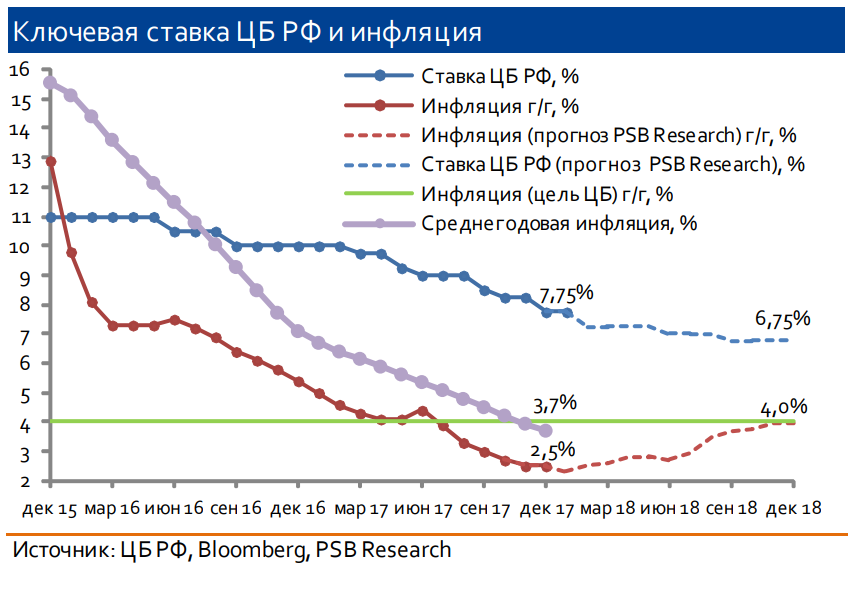 Затем мы используем коэффициенты дисконтирования, подразумеваемые кривой YC — , чтобы вычислить соответствующую теоретическую цену грязной облигации B — .
Затем мы используем коэффициенты дисконтирования, подразумеваемые кривой YC — , чтобы вычислить соответствующую теоретическую цену грязной облигации B — .
Точно так же кривая доходности YC + строится путем повышения начальной нулевой ставки i th z i вверх на заданную величину δ с сохранением всех остальных фиксированные ставки ввода. Затем мы используем коэффициенты дисконтирования, подразумеваемые кривой YC + , чтобы вычислить соответствующую теоретическую цену грязной облигации B + .
Это определение / построение K i имеет следующие два следствия:
Следствие 1: Для суммы K = K 1 + K 2 +… + K N должен содержать:
K = (B ΄ — -B ΄ + ) / (2B δ)
где B ΄ — и ΄ + — цены облигаций, возникающие в результате параллельного смещения вниз и, соответственно, вверх кривой базовой доходности YC , в результате чего все входные нулевые ставки одновременно смещаются на заданную величину δ .
Следствие 2: Когда сдвиг ставки δ стремится к 0 , сумма длительностей ключевой ставки K должна стремиться к Модифицированной дюрации D облигации.
Создание объекта облигации с фиксированной ставкой в Excel
Мастер Deriscope может сгенерировать формулу электронной таблицы, которая создает объект облигации с фиксированной ставкой в Excel, как показано на следующем видео:
Ниже показано, как выглядит вставленная формула: после того, как я сдвинул два блока вверх, чтобы все они были видны.Я также изменил в электронной таблице исходный созданный мастером расчетный день по умолчанию 0 на 2 , чтобы получить более реалистичную облигацию, которая рассчитывается на 2 рабочих дней после даты сделки 06 декабря 2018 г. (сегодня). Из той же мотивации к реализму я также изменил исходные созданные мастером Начало и Конец Даты , чтобы облигация начала накапливаться в прошлом и, следовательно, на сегодняшний день существует ненулевая сумма начисления, которая делает пятно грязным, а чистые цены неравными.Наконец, я установил DayCount на 30/360 , чтобы иметь нетривиальные вычисления доли года для всех задействованных временных интервалов.
Понимание формулы
Как видите, ячейка A1 содержит формулу = ds (A2: B15) , которая принимает один входной аргумент и возвращает текст & FxdBnd_A1: 1. 3
3
Префикс и указывает что & FxdBnd_A1: 1.3 — это дескриптор некоторого объекта.Фактически он указывает на объект типа Облигация с фиксированной процентной ставкой и может использоваться в любом контексте, где ожидается объект типа Облигация , поскольку тип Облигация с фиксированной ставкой наследуется от Облигации .
Диапазон ввода A2: B15 содержит 12 пар ключ-значение с очевидными значениями.
Тем не менее, я могу прочитать информацию, относящуюся к каждой паре ключ-значение , вне мастера, просто выбрав соответствующую ячейку.
Что касается значений , обозначенных синим цветом, я могу редактировать их, вводя вручную в ячейки или используя мастер, как описано в предыдущих статьях, например здесь.
График начислений фиксированной части облигации представлен как объект типа График в ячейке B9 . Он генерируется отдельно по формуле = ds (D2: E17) в ячейке D1 , на которую ссылается B9 .
Наконец, соглашения, характеризующие фиксированную ставку 4% , предоставляются объектом типа Простая ставка , созданным в ячейке D18 .Как видите, купон по облигации начисляется в соответствии с соглашением о простом начислении сложных процентов.
Расчет доходности облигации и грязной цены
Как я объяснил выше, для расчета KRD мне нужно узнать текущую доходность. Предположим, что чистая цена облигации на данный момент составляет 95 . Я могу использовать мастер для создания двух формул, которые вычисляют доходность и грязную цену из заданной чистой цены.
Я могу использовать мастер для создания двух формул, которые вычисляют доходность и грязную цену из заданной чистой цены.
Мастер создает эти формулы, используя входные данные по умолчанию для чистой цены 100 .После того, как формулы были вставлены в электронную таблицу, я меняю их на 95 (фактически связывая соответствующие ячейки с другой отдельной ячейкой, предназначенной для хранения моей чистой цены).
Мастер также строит условные обозначения нормы доходности таким образом, чтобы она составляла непрерывно составляла и имела тот же DayCount , что и у вызывающего объекта Bond. Поскольку у последнего был DayCount из 30/360 , мастер выбирает то же самое, как вы видите в ячейке E17 ниже.
Поскольку в этих двух формулах не указана ссылочная дата, отображаемые результаты 5.1441% и 97.222222 представляют собой доходность и грязную цену соответственно на дату погашения облигации, то есть 2 рабочих дней в будущем.
Построение базовой кривой доходности
Моя следующая задача — построить кривую доходности из непрерывно составных нулевых ставок, которые все равны моей только что рассчитанной доходности 5.1441%. Все мои нулевые ставки будут спотовыми без каких-либо задержек в расчетах. Поскольку они равны друг другу и непрерывно составные , их подразумеваемые форвардные начаты непрерывно составные нулевые ставки также будут плоскими и равными 5,1441% . Таким образом, нет никаких расхождений из-за того, что доходность 5,1441% была рассчитана с датой начала на два рабочих дня в будущем.
Проще начать с того, что попросите мастера сгенерировать формулу электронной таблицы, которая создает кривую доходности из нулевых ставок, как показано в следующем видео:
Мастер вставляет слишком много дополнительных входных данных в электронную таблицу, поэтому я иду вперед, и я удаляю то, что мне не нужно для большей ясности.
Также я меняю моделированное количество с Форвардная ставка на Нулевая доходность , так как я хочу иметь плоскую (независимую от срока погашения) нулевую ставку, и это может быть лучше всего достигнуто, когда мое моделированное количество — относительно в котором происходит вся интерполяция — представлена нулевой скоростью.
Также я связываю обе записи DayCount с облигацией DayCount , указанной в ячейке B29 , и, наконец, добавляю еще 3 сроков погашения, чтобы достичь 5-летнего горизонта , охватываемого интервалами в один год.
После того, как я связал все входные нулевые ставки с ячейкой D3 , содержащей мою расчетную доходность по облигациям, моя таблица будет выглядеть так:
Теперь я должен убедиться, что моя кривая доходности построена правильно в том смысле, что она должна воспроизводить грязные Цена облигации 97.222222 рассчитывается в ячейке D18 .
Deriscope предлагает два способа расчета приведенной стоимости облигации по заданной кривой доходности. Обычный способ — позволить мастеру сгенерировать формулу электронной таблицы, которая вызывает функцию Price , которая доступна для всех объектов типа Tradable и, следовательно, для моего объекта типа Bond , который наследуется от Tradable — создан в ячейке A1 .
Более простой подход — использовать специальную функцию Dirty Price , которая доступна только для объектов типа Bond . Поэтому я сначала выбираю ячейку A1 , чтобы сообщить мастеру, что я хочу использовать функции, применяемые к выбранному объекту Bond , а затем перехожу к селектору функций мастера, где выбираю Dirty Price функция. Наконец, я выбираю пустую ячейку D23 и нажимаю кнопку Go , чтобы вставить сгенерированную формулу в эту ячейку.
В этом видео вы могли заметить, что мастер также создает новую кривую доходности с фиксированной ставкой 4% для использования в качестве единственного необходимого ввода для функции Грязная цена . Он не связан с существующей кривой доходности, уже созданной в ячейке G1 , потому что он понимает, что последняя кривая отличается (не плоская 4% ) от кривой, созданной внутри компании. Мастер позволяет избежать ненужного создания формул электронной таблицы только в том случае, если найдена существующая формула, которая создает объект, точно соответствующий создаваемому.Это причина, по которой мастер решает в этом случае продолжить создание еще одной формулы для построения кривой доходности.
После этого я удаляю эту новую сгенерированную кривую и просто связываю ячейку E27 с моей существующей кривой в ячейке G1 .
Вот как теперь выглядит моя таблица. Он содержит дополнительную формулу, которая производит вывод цены грязной облигации в ячейке D23 :
Разрешение несоответствия грязной цены
Итак, у нас есть проблема!
Грязная цена вне кривой доходности составляет 99. 219255 в ячейке D23 , которая отличается от истинной цены облигации 97.222222 , рассчитанной в ячейке D18 !
219255 в ячейке D23 , которая отличается от истинной цены облигации 97.222222 , рассчитанной в ячейке D18 !
Вы можете подумать, что здесь задействован другой временной интервал расчетов.
Расчетное время в несколько дней никогда не приведет к такой огромной разнице в цене. Фактически, обе цены рассчитываются относительно 2 рабочих дней с сегодняшнего дня, потому что функция Dirty Price всегда вычисляет грязную цену относительно даты расчетов по облигации, если в качестве входных данных явно не указана ссылочная дата.Это сохраняется независимо от того, используется ли функция с входом Clean Price — как в ячейке D18 — или с входом Discount Curve — как в ячейке D23 .
Виновник в другом.
Хотя кривая доходности построена на основе плоских нулевых ставок, она совсем не плоская! По умолчанию предполагается, что все пять нулевых скоростей, представленные в качестве входных данных в диапазоне столбцов h30: h34 , соответствуют соглашению простого сложения .Это означает, что соответствующие ставки непрерывно составные становятся все меньше и меньше по мере увеличения срока погашения. Эти убывающие ставки затем используются в качестве привязки для расчета непрерывной ставки сложного для любого другого срока погашения посредством линейной интерполяции. Конечный эффект заключается в том, что кривая доходности с бутстрепом представляет собой непрерывное уменьшение сложенных нулевых ставок и, следовательно, менее интенсивно дисконтирует будущие денежные потоки по облигации. В результате в ячейке D23 отображается более высокая предполагаемая приведенная стоимость облигации.
В результате в ячейке D23 отображается более высокая предполагаемая приведенная стоимость облигации.
Решение на самом деле простое: вместо того, чтобы вводить одно и то же число 5.1441% во все ячейки диапазона h30: h34 , вычислите и введите эквивалент непрерывно сложная ставка для каждого срока погашения.
По определению, в течение интервала времени t , просто начисленная ставка r, действующая на одну денежную единицу, начисляет процентную сумму rt , тогда как непрерывно начисляемая ставка c начисляет сумму процентов e ct -1 .Две ставки – и – считаются эквивалентными по отношению к заданному временному интервалу –, если они генерируют точно такую же сумму процентов в течение этого интервала. Обратите внимание, что две эквивалентные ставки относительно определенного временного интервала t , как правило, не будут эквивалентны относительно другого временного интервала t ΄ .
Таким образом, чтобы ставки были эквивалентными, мы должны иметь rt = e ct -1 => r = (e ct -1) / t .
Мы знаем, что c = 5,1441% для всех сроков погашения, но как рассчитать временной интервал t для каждого срока погашения с нулевой процентной ставкой?
Временной интервал t относится к времени между датой начала соответствующего депозитного договора и датой его окончания. Итак, нам нужно сначала найти эти две даты.
Итак, нам нужно сначала найти эти две даты.
Ниже вы видите раздел моей электронной таблицы с двумя дополнительными столбцами, в которых рассчитываются дата окончания и временной интервал для каждой входной записи нулевой ставки.Как обычно, я использую простые формулы Deriscope для получения результатов:
Новая кривая доходности принимает в качестве входных данных увеличение , просто сложенные ставки , предварительно рассчитанные для соответствия той же постоянной ставке с непрерывным составом , равной 5,1441%. Следовательно, это плоская непрерывно сложенная кривая нулевой ставки . Действительно, подразумеваемая кривой цена грязной облигации оказывается теперь почти равной фактической цене облигации, как видно на следующем изображении:
Построение повышенных кривых доходности
Моя следующая задача — построить 10 дополнительных кривых доходности.
Для каждого срока погашения с нулевой процентной ставкой должны быть построены две новые кривые доходности. Один соответствует нисходящей нулевой скорости с непрерывным составом , а другой соответствует нисходящей нисходящей скорости с непрерывным составлением .
Итак, сначала я представляю два столбца с заголовками r- и r + , которые содержат увеличенные и увеличенные значения , просто составившие нулевые ставки соответственно, как показано ниже:
Затем я представляю еще два столбца с заголовком yc — и yc + , которые содержат соответствующие объекты кривой доходности .Они создаются с помощью немного сложных формул, которые полагаются на индекс строки, предоставленный в дополнительном столбце, вставленном слева от них, как показано ниже:
Я ввел мышью внутри формулы в ячейке P20 , чтобы вы могли легко увидеть зависимые диапазоны. Создание объекта «Кривая доходности » с рельефом — это простое применение функции Deriscope Clone . Как вы видите выше, функция Clone применяется к базовому объекту кривой доходности ячейки G1 и пытается изменить его значение, связанное с ключом Deposit Set = в ячейке G18 .Все это передают первые три входных аргумента формулы ds .
Создание объекта «Кривая доходности » с рельефом — это простое применение функции Deriscope Clone . Как вы видите выше, функция Clone применяется к базовому объекту кривой доходности ячейки G1 и пытается изменить его значение, связанное с ключом Deposit Set = в ячейке G18 .Все это передают первые три входных аргумента формулы ds .
Жесткая часть — это последний входной аргумент, который предоставляет новое значение Deposit Set , которое должен содержать созданный клонированный объект.
Обратите внимание, что исходное значение — это таблица, определенная в диапазоне G19: h34 . Я хочу, чтобы мое новое значение было той же таблицей, за исключением элемента 5.2788% во второй строке и втором столбце . Я также хочу, чтобы мой клонированный объект Yield Curve ссылался на пониженную скорость 4.2312% дано в ячейке M20 .
На самом деле вопрос таков: как я могу создать другую таблицу, которая является копией исходной таблицы, за исключением одной ячейки?
Ответ дается специальной формулой электронной таблицы Deriscope Replace , имеющей следующий синтаксис:
= Replace (OldTable, FromRow, ToRow, FromColumn, ToColumn, NewSubTable)
The OldTable Table и New аргументы — это прямоугольные наборы данных, а все остальные аргументы — целые числа.
Чтобы заменить ставку 5,2788% на 4,2312% , требуется формула:
= Заменить (19 долларов США: 24 доллара США; 2; 2; 2; 2; 4,2312%)
Принимая более общий формат, который может быть скопирован, последний аргумент ds , наконец, становится:
dsReplace ($ G $ 19: $ H $ 24; $ O20; $ O20; 2; 2; M20)
Строительство повышенных цен на грязные облигации и соответствующих значений KRD
Теперь, когда мне удалось построить кривые с повышенными отметками, я могу ввести еще два столбца, которые содержат соответствующие подразумеваемые цены грязных облигаций на дату расчетов по облигациям, как показано ниже:
Последний шаг — добавить последний столбец со значениями KRD, рассчитанными в соответствии с их определением K i = (B — -B + ) / (2Bδ) , как показано ниже:
. обратите внимание на значение 5Y KRD, равное 1.750373 меньше значения 4Y KRD, равного 2,099922 . Это связано с тем, что облигация 5 лет началась примерно 6 месяцев назад и, следовательно, имеет срок погашения примерно на 6 месяцев до привязки к погашению с нулевой ставкой 5 лет , относительно которой рассчитывается 5 лет KRD. На существенную выплату основного долга по облигации в 4 ½ лет влияет только половина скачка нулевой ставки 5Y , и поэтому его вклад становится только половиной того, что мог бы быть, если бы две привязки дат совпали.Кроме того, все купоны, выплаченные до наступления срока погашения, добавляют нулевой вклад к этой цифре 5Y KRD.
обратите внимание на значение 5Y KRD, равное 1.750373 меньше значения 4Y KRD, равного 2,099922 . Это связано с тем, что облигация 5 лет началась примерно 6 месяцев назад и, следовательно, имеет срок погашения примерно на 6 месяцев до привязки к погашению с нулевой ставкой 5 лет , относительно которой рассчитывается 5 лет KRD. На существенную выплату основного долга по облигации в 4 ½ лет влияет только половина скачка нулевой ставки 5Y , и поэтому его вклад становится только половиной того, что мог бы быть, если бы две привязки дат совпали.Кроме того, все купоны, выплаченные до наступления срока погашения, добавляют нулевой вклад к этой цифре 5Y KRD.
Сходимость суммы KRD к модифицированной продолжительности
Как упоминалось ранее, сумма значений KRD K = K 1 + K 2 +… + K N должна равняться (B ΄ — -B ΄ + ) / (2 δ) , где B ΄ — и B ΄ + цены облигаций, полученные из параллельный сдвиг базовой кривой доходности вниз и, соответственно, вверх, в результате чего все входные нулевые ставки сдвигаются одновременно посредством заданного одностороннего сдвига ставки & delta; .
Следовательно, если мои вычисления были правильными, сумма K должна сходиться к Modified Duration , поскольку сдвиг скорости δ приближается к 0 .
Сумма получается 4.067035 .
Модифицированная длительность вычисляется с помощью соответствующей функции Deriscope для значения 4.066705 , как показано ниже:
Все еще при одностороннем сдвиге скорости 1% (как показано в ячейке N18 ) два результаты очень близки друг к другу.Оказалось, что схождение — почти подозрительно — идеальное и очень быстрое. Например, мы можем достичь согласия до первых 10 десятичных цифр, установив для параметра Rate Shift такое низкое значение, как 0,0001% , как показано ниже:
Эффективность: получение тех же результатов за один шаг с помощью функции Deriscope KRD
Представьте, что вы хотите рассчитать значения KRD для сотен облигаций или изменить количество контрольных сроков погашения KRD.Представленное ранее решение для работы с электронными таблицами явно непрактично.
Deriscope предоставляет функцию под названием KRD , которая выполняет все эти шаги намного более эффективно благодаря своей реализации на C ++ и предоставляет окончательные результаты.
Просто выберите ячейку A1 , которая содержит объект Bond, чтобы предупредить мастера о своем желании работать с объектом типа Bond. Затем перейдите к средству выбора функций в области мастера, выберите функцию KRD и нажмите кнопку «Перейти», чтобы вставить сгенерированную формулу в электронную таблицу.Результат показан ниже:
Как вы видите, мастер принял Чистую цену 100 , сдвиг ставки 1% и 7 привязок срока погашения. Затем вывод передается по формуле массива = ds (P27: Q33; S27: S34) в диапазоне T28: T34 . Затем я меняю чистую цену на 95 и сбрасываю входные сроки погашения на пять сроков погашения, которые я использовал ранее. Я также изменяю ячейку сдвига скорости N18 обратно на 1% , чтобы и мои формулы электронной таблицы, и этот новый прямой вывод Deriscope полагались на одни и те же входные данные.Ниже приведен результат, подтверждающий, что функция Deriscope KRD обеспечивает те же значения KRD, что и решение для работы с электронными таблицами:
Затем вывод передается по формуле массива = ds (P27: Q33; S27: S34) в диапазоне T28: T34 . Затем я меняю чистую цену на 95 и сбрасываю входные сроки погашения на пять сроков погашения, которые я использовал ранее. Я также изменяю ячейку сдвига скорости N18 обратно на 1% , чтобы и мои формулы электронной таблицы, и этот новый прямой вывод Deriscope полагались на одни и те же входные данные.Ниже приведен результат, подтверждающий, что функция Deriscope KRD обеспечивает те же значения KRD, что и решение для работы с электронными таблицами:
Полный отчет KRD
Если я изменю значение FALSE в ячейке Q33 на TRUE , формула ds вернет объект, содержащий несколько промежуточных результатов, которые я затем могу вставить в электронную таблицу или просматривать их через мастера. Ниже я продублировал формулу Deriscope KRD , на этот раз с Full Report = TRUE , и я выбираю выходную ячейку, чтобы мастер отображал ее содержимое:
Вы заметили, что помимо 5 Значения KRD показаны в третьей строке сверху, также указаны некоторые другие представляющие интерес величины.
Например, погашение облигации 10.12.2018 , доходность 0,05144 , базовая нулевая кривая, которая использовалась для расчетов, грязная цена, подразумеваемая базовой нулевой кривой 97,22 , фактическая грязная цена также 97,22 , которая является результатом прибавления текущего начисления к данной чистой цене, All Rates Duration , что соответствует (B ΄ — -B ΄ + ) / (2B δ) , упомянутое выше для заданного сдвига скорости δ из 1% , сумма значений KRD и модифицированной продолжительности .
Еще более подробную информацию можно получить, щелкнув значок маленькой линзы справа от Details = следующим образом:
Здесь вы можете увидеть и, при желании, перенести в электронную таблицу все нисходящие и восходящие кривые доходности, которые использовались в расчет KRD, соответствующие предполагаемые цены грязных облигаций и итоговые значения KRD. Нижняя строка со сроком погашения % 0D содержит кривые увеличенной доходности, полученные путем одновременного параллельного сдвига всех нулевых ставок, соответствующих подразумеваемых цен грязных облигаций и псевдо-KRD, который теперь отражает все ставки вместе.
Вы можете скачать электронную таблицу, созданную с помощью описанных выше шагов, здесь.
Не стесняйтесь обращаться ко мне, если вы хотите поделиться какими-либо мыслями относительно этого продукта или если вы хотите запросить какие-либо конкретные функции. Контактная информация и ссылки на социальные сети доступны на моем веб-сайте https://www.deriscope.com
Экзамен уровня I CFA 2021: подготовка к исследованию CFA
Срок действия облигации измеряет чувствительность полного изменения цены к изменению процентных ставок.
- Дюрация доходности Статистика измеряет чувствительность полной цены облигации к ее собственной доходности к погашению. Они включают дюрацию Маколея, модифицированную дюрацию, денежную дюрацию и ценовую стоимость базисного пункта.
- Кривая дюрации Статистика измеряет чувствительность полной цены облигации к эталонной кривой доходности, например, эффективной дюрации.
Дюрация — это средневзвешенное время для получения приведенной стоимости каждого купонного и основного платежа по облигации.Например, облигация с дюрацией три означает, что в среднем требуется три года, чтобы получить приведенную стоимость денежных потоков по облигации.
Маколей Продолжительность
Фредерик Маколей разработал концепцию продолжительности примерно 80 лет назад. Он продемонстрировал, что дюрация облигации является более подходящей мерой временных характеристик, чем срок до погашения облигации, поскольку дюрация включает как погашение капитала при погашении, так и размер купона, и сроки выплат.Дюрация Маколея определяется как средневзвешенное время до полного возмещения основной суммы и процентных платежей. Веса — это акции по полной цене, соответствующей каждому купону и выплате основной суммы.
Он продемонстрировал, что дюрация облигации является более подходящей мерой временных характеристик, чем срок до погашения облигации, поскольку дюрация включает как погашение капитала при погашении, так и размер купона, и сроки выплат.Дюрация Маколея определяется как средневзвешенное время до полного возмещения основной суммы и процентных платежей. Веса — это акции по полной цене, соответствующей каждому купону и выплате основной суммы.
В качестве альтернативы дюрацию Маколея можно рассчитать с использованием формулы закрытой формы.
Модифицированная длительность
Модифицированная дюрация показывает, как цены облигаций движутся пропорционально небольшим изменениям доходности. В частности, модифицированная дюрация оценивает процентное изменение цены облигации с изменением доходности.-D mod = модифицированная дюрация для облигации
Di = изменение доходности в базисных пунктах, деленное на 100
P = начальная цена облигации
Модифицированная дюрация предполагает, что соотношение цена / доходность является прямой линией. Однако соотношение цена / доходность является выпуклым, а не линейным. Предположим, что облигация имеет начальную доходность 0 иен. К соотношению цена / доходность можно провести касательную по Y 0 . Наклон касательной зависит от дюрации облигации.Если доходность упадет до 1 иен, цена вырастет до 1 иен. Из-за линейного допущения изменение цены, измеренное дюрацией, составляет 2 песо — 0 песо.
Примерная измененная продолжительность:
V — = цена при снижении доходности
V + = цена при увеличении доходности
V 0 = начальная цена
Например, рассмотрим продажу 20-летней безопциональной облигации с купоном 9% по цене 134,6722 с доходностью 6%. Если доходность уменьшится на 20 базисных пунктов с 6.0% до 5,8%, цена увеличится до 137,5888. Если доходность увеличится на 20 базисных пунктов, цена упадет до 131,8439. Таким образом: ApproxModDur = (137,5888 — 131,8439) / (2 x 134,6722 x 0,002) = 10,66. Это говорит о том, что при изменении требуемой доходности на 1% цена облигации изменится примерно на 10,66%.
Таким образом: ApproxModDur = (137,5888 — 131,8439) / (2 x 134,6722 x 0,002) = 10,66. Это говорит о том, что при изменении требуемой доходности на 1% цена облигации изменится примерно на 10,66%.
Продолжительность Маколея математически связана с модифицированной продолжительностью.
Облигация с дюрацией Маколея 10 лет, доходностью к погашению 8% и полугодовыми выплатами будет иметь модифицированную дюрацию:
Dmod = 10 / (1 + 0.08/2) = 9,62 года
Эффективная длительность
Эффективная дюрация измеряет процентный риск с точки зрения изменения эталонной кривой доходности . Это очень похоже на приблизительную измененную продолжительность.
Модель ценообразования может использоваться для оценки изменения цены в результате изменения эталонной кривой доходности, а не собственной доходности облигации к погашению. V- и V + корректируются, чтобы отразить любые изменения в денежных потоках (из-за встроенных опционов), которые возникают в результате изменения базовой кривой доходности.Для облигаций со встроенными опционами следует использовать эффективную дюрацию.
Длительность ключевой скорости
Важно отличать риск процентной ставки от риска кривой доходности.
- Риск процентной ставки — это чувствительность облигации к параллельным сдвигам кривой доходности.
- Риск кривой доходности — это чувствительность облигации к изменениям формы кривой доходности.
Параллельные сдвиги кривой доходности случаются редко. Аналитик может захотеть измерить изменение цены облигации, изменив спотовую ставку для определенного ключевого срока погашения и поддерживая постоянную спотовую ставку для других ключевых сроков погашения.Дюрация ключевой ставки — это чувствительность стоимости облигации к изменениям одной спотовой ставки, при этом все остальные спотовые ставки остаются неизменными. Для каждой точки кривой спотовой ставки существует дюрация ключевой ставки, поэтому существует вектор дюрации, представляющий каждый срок погашения на кривой спот-ставки.
Тема отмечена как завершенная.
Тема отмечена как неполная.
Тема добавлена в закладки для последующего просмотра на вашей панели управления.
Закладка удалена с панели управления.
Дюрация муниципальных облигаций по ключевой ставке
Лицензия
СОГЛАШЕНИЕ ОБ АВТОРСКИХ ПРАВАХ
Автор: _____________________________________________________________________________________ («Автор)
Адрес и телефон: _________________________________________________________________________________________
Название статьи: _________________________________________________________________________________ (« Статья »)
Journal: The Journal of ________________________________________________________________________
Пожалуйста, укажите тип работы:
□ Собственная работа автора □ Работа правительства США □ Работа сделанная по найму
Настоящим автор отправляет статью в Pageant Media Ltd./ «Исследование управления портфелем» (PMR) для публикации в журнале. Подписание этого документа представляет и гарантирует, что (i) он или она уполномочены передавать авторские права на Статью и (ii) ни Статья, ни настоящее Соглашение об авторском праве не нарушают какие-либо права какой-либо другой стороны. Автор настоящим переуступает и передает PMR авторские права на Статью и на нее во всем мире. Все другие права интеллектуальной собственности, относящиеся к статье, остаются за Автором . Автор понимает, что PMR имеет право использовать Статью без ограничений любым способом и в любых средствах массовой информации, известных в настоящее время или в дальнейшем изобретенных или разработанных. Если PMR намеревается внести какие-либо изменения в содержание опубликованной статьи, необходимо получить предварительное письменное разрешение от Автора.
PMR предоставляет Автору следующие неисключительные права:
- Право публиковать на внутренних или внешних веб-сайтах название статьи и аннотацию вместе со ссылкой на опубликованную статью на веб-сайте PMR.В связи с такой публикацией Автор должен включить уведомление об авторских правах, по существу, в следующей форме: «© [год публикации] PMR. Все права защищены.»
- Право использовать диаграммы, таблицы и рисунки из статьи на слайдах презентации, но не в статьях, главах книг или аналогичных форматах, состоящих в основном из текстового содержания.
Автор должен удалить все версии Статьи до публикации со всех веб-сайтов (включая SSRN и ResearchGate).
Автор понимает и соглашается с тем, что, за исключением случаев, указанных выше, любое использование, воспроизведение или распространение статьи строго запрещено, если не согласовано в письменной форме с PMR. Без ограничения общего характера вышеизложенного, Автор не имеет права (i) публиковать Статью в какой-либо службе обмена файлами (включая SSRN и ResearchGate), (ii) распространять Статью на любых научных или отраслевых конференциях или подобных мероприятиях, (iii) включить статью в пакет учебных курсов или аналогичный сборник, или (iv) разрешить перепечатку статьи в качестве главы книги. В случае, если Автор нарушает вышеупомянутые ограничения на использование, воспроизведение или распространение Статьи, Автор соглашается выплатить PMR убытки, равные действующей на тот момент ставке PMR за неограниченное распространение прав на Статью на время нарушения.
Автор не имеет права публиковать или распространять какие-либо обновления, сиквелы или другие работы, основанные или производные от Статьи, если такое обновление, продолжение или другая работа не содержит как минимум одной трети нового контента.
Автор гарантирует наличие необходимого письменного разрешения на воспроизведение в статье и в журнале как печатной, так и электронной версии любого текста, экспонатов или других материалов от первоначального правообладателя или соответствующих органов. Автор подтверждает, что статья является оригинальной работой, не нарушает права интеллектуальной собственности третьих лиц и не может быть истолкована как плагиат другой опубликованной работы. Автор утверждает, что статья не содержит оскорбительных, дискредитирующих, клеветнических, непристойных, мошеннических заявлений, не нарушающих права других лиц, незаконных или нарушающих применимое законодательство.
Любые изменения в этом соглашении будут считаться недействительными, если они не согласованы в письменной форме с PMR.
______________________________________________________ ____________________
Подпись автора Дата
______________________________________________________ ____________________
Подпись представителя компании * Дата
Если работа сделана по найму
* Если оставлено пустым Подпись автора будет автоматически принята как представитель компании
Если Статья уже публиковалась или подавалась в публикацию ранее в любой форме, обратите внимание, где | p |
Чтобы получить подробное объяснение того, как вы можете использовать версии вашей статьи до и после публикации, посетите https: // www.pm-research.com/permissions-and-reprints
Когда складываются показатели ключевой ставки?
Дюрация и выпуклость ключевых процентных ставок измеряют риск вашего портфеля в отношении изменений конкретных ключевых процентных ставок. Но когда отдельные значения продолжительности и выпуклости складываются в ваши общие показатели, основанные на параллельных сдвигах? И насколько хорошо дельта- и гамма-векторы отражают природу лежащих в основе облигаций? Мы посчитали и дадим вам несколько (удивительно?) Ответов и дальнейшее понимание этой темы.
Дюрация и выпуклость — это классические меры чувствительности цены облигации к параллельному изменению процентных ставок, и как таковые они являются фундаментальными факторами управления рисками в вашем портфеле. Однако они не предоставляют вам информацию о рисках, связанных с реальными непараллельными сдвигами кривой доходности.
Дюрация и выпуклость ключевой ставки — это один из способов измерения ожидаемых изменений цены облигаций в результате произвольных сдвигов кривой доходности.В 1992 г. Thomas Ho 1 ввел дюрации ключевой ставки как чувствительность цены к изменениям ключевых ставок с конкретными сроками погашения, полученную путем применения серии треугольных сдвигов к спотовой ставке в ключевые моменты срока погашения. Треугольные сдвиги построены так, что они суммируются с параллельным сдвигом кривой доходности. На рисунке 1 показан набор треугольных сдвигов спотовых ставок.
Рисунок 1 — Треугольные сдвиги спотовой ставки размером h, определяемые сроками погашения 2Y, 5Y.7Y и 10Y.
Показатели ключевой ставки приводят к нескольким интересным вопросам, многие из которых нам также часто задают наши клиенты, и мы ответим на два наиболее распространенных в этом блоге:
- Сдвиг кривой доходности, лежащий в основе показателей ключевой ставки, в точности соответствует параллельному смещению, но при каких обстоятельствах дюрации / выпуклость ключевой ставки суммируются в точности с дюрацией / выпуклостью?
- Показывают ли векторы чувствительности разумное распределение по срокам погашения ключевой ставки относительно характера рассматриваемой облигации?
Если вас интересует более глубокий анализ, ознакомьтесь с нашим техническим документом Scanrate Model Service 2018 по теме, доступной для подписчиков Scanrate Model Service на Scanrate Model Service
Расчет дюрации и выпуклости ключевой ставки
Для расчета показателей риска ключевой ставки нам необходимо применить дискретизацию дюрации и выпуклостей, поскольку, как правило, нет решений в закрытой форме. 2 Использование приближений неизбежно приводит к ошибке дискретизации, которая может различаться по размеру и знаку в зависимости от используемого метода. Небольшая ошибка приводит к высокой точности приближения. 2} = \ frac {\ frac {P (s (h )) — P} {h} — \ frac {PP (s (-h))} {h}} {h} $$
Когда сдвиг \ (s \) параллелен, приведенные выше формулы определяют продолжительность и выпуклость, тогда как отдельные длительности / выпуклости ключевой скорости находятся, когда \ (s \) представляет собой треугольный (или аналогичный) сдвиг.
Расчет смены в сумме
Показатели ключевой ставки, основанные на треугольных сдвигах, не всегда суммируют , а не с соответствующими параллельными показателями, как показано ниже. Однако можно определить набор сдвигов, обладающий этим качеством. Мы обозначаем эти сдвиги с корректировкой влево и вправо и представляем их ниже.
Основная идея состоит в том, чтобы «начать» с несмещенной кривой, а затем «пройти» по срокам погашения ключевой ставки, используя набор сдвигов, которые постепенно сдвигают все большую часть кривой доходности и, наконец, «заканчивают» полностью. параллельный сдвиг по последней ключевой ставке.Для сдвигов, скорректированных влево, начало находится влево, то есть движение происходит от наименьшего к наибольшему сроку погашения ключевой ставки, в то время как сдвиги, скорректированные вправо, начинаются вправо при наибольшем сроке погашения ключевой ставки, перемещаясь влево к наименьшему сроку погашения.
Сдвиги спроектированы таким образом, что разница между двумя последовательными сдвигами составляет соответствующий треугольный сдвиг. Таким образом, каждый показатель ключевой ставки определяется с использованием разницы в цене двух последовательных сдвигов, связанных с его сроком погашения.Интуитивно понятно, что итоговые показатели ключевой ставки складываются, потому что промежуточные цены уравновешиваются, оставляя только разницу между начальной и конечной ценами на основе нулевого и полного параллельного сдвига.
На рис. 3 показан пример сдвигов с поправкой влево и вправо, используемых для расчета значений ключевой ставки 5Y. Сдвиги названы в честь срока погашения ключевой ставки, при котором сдвиг прерывается от параллельного движения к линейному снижению.
Рис. 3. Сдвиги спот-ставок, скорректированные влево (вверху) и сдвиги, скорректированные вправо (внизу), используемые для расчета показателей ключевой ставки при сроке погашения 5 лет.h_ {N + 1}) = — \ frac {P_p-P} {h} = DV01_ {1s} $$
Первое равенство следует из определения продолжительности ключевой ставки, второе равенство следует, поскольку сумма складывается и, следовательно, исключает все промежуточные цены. Третье равенство следует потому, что набор сдвигов с поправкой вправо начинается справа с несмещенной кривой и заканчивается влево с полностью смещенной кривой. Окончательное равенство — это само определение (дискретизированной) долларовой дюрации.
Аналогичные аргументы применимы для сдвигов, скорректированных влево, где первый сдвиг слева — это несмещенная кривая, а последний сдвиг вправо — параллельный.Рассуждения также распространяются на случай двусторонней продолжительности и выпуклости.
Когда складываются показатели ключевой ставки?
На основе набора ключевых ставок, размещенных со сроками погашения 1Y, 2Y, 5Y, 7Y, 10Y, 20Y и 30Y, мы сравниваем долларовую дюрацию и выпуклость с суммой долларовой дюрации и выпуклости ключевой ставки. Инструмент представляет собой датскую государственную облигацию без права отзыва 4,5% -2039 с маркированным профилем (DK00090), результаты представлены в таблице 1.
| ПЕРЕКЛЮЧЕНИЕ КЛЮЧА | \ (DV01_ {1s} \) | $$ \ displaystyle \ sum_ {i} DV01_ {1s, i} $$ | \ (DV01_ {2s} \) | $$ \ displaystyle \ sum_ {i} DV01_ {2s, i} $$ | $$ C _ \ $$$ | $$ \ displaystyle \ sum_ {i} C _ {\ $, i} $$ |
|---|---|---|---|---|---|---|
| Треугольник | 24,9549 | 25,0268 | 25.2038 | 25.2030 | 4,9782 | 3.5242 |
| С левой регулировкой | 24,9549 | 24,9549 | 25.2038 | 25.2038 | 4,9782 | 4,9782 |
| С правой регулировкой | 24,9549 | 24,9549 | 25.2038 | 25.2038 | 4,9782 | 4,9782 |
| Среднее значение с поправкой влево и вправо | 24.9549 | 24,9549 | 25.2038 | 25.2038 | 4,9782 | 4,9782 |
Таблица 1 — Сравнение дюрации и выпуклости доллара с суммой ключевой ставки доллара и выпуклости, соответственно. Сроки погашения ключевой ставки — 1 год, 2 года, 5 лет, 7 лет, 10 лет, 20 лет и 30 лет. Инструмент представляет собой датскую государственную облигацию без права отзыва на сумму 4,5% -2039. Различия выделены жирным шрифтом. Цифры рассчитаны на 15 февраля 2018 г.
Мы посчитали и обнаружили, что результаты являются общими для облигаций без права отзыва. Таким образом, основные выводы:
Ключевые результаты при сложении длительностей и выпуклостей ключевых ставок
|
Все дело в выпуклости
Из приведенного выше примера мы узнали, что дюрации ключевой ставки не суммируются с дюрацией при использовании треугольных сдвигов, даже для облигации без встроенной опционности. * + h \).* \). Цена изменяется на \ (\ Delta P_5 \) при применении пятилетнего треугольного сдвига, а семилетний треугольный сдвиг приводит к изменению цены на \ (\ Delta P_7 \). Из графической иллюстрации ясно, что сумма этих двух изменений цен больше, чем изменение цены от параллельного сдвига \ (\ Delta P_P \). Математически это происходит из-за выпуклости соотношения цена-доходность, подчиняющейся неравенству Дженсена. В результате долларовые дюрации ключевой ставки составляют , а не сумм к долларовой дюрации, и мы переоцениваем фактическое изменение цены при суммировании односторонних частичных дюраций при положительной выпуклости.
Рисунок 5 — Соотношение цены и доходности бескупонной облигации, включая изменения цен, полученные в результате полного параллельного сдвига, \ (\ Delta P_P \), а также изменения цен в результате треугольных сдвигов в 5Y и 7Y, \ (\ Delta P_5 \) и \ (\ Delta P_7 \) соответственно.
Некоторые заключительные замечания:
- Пример касается бескупонной облигации, то есть разовой выплаты. Однако облигация без права отзыва может рассматриваться как серия облигаций с нулевым купоном, и поэтому аргументы распространяются на облигации без права отзыва в целом.Смещение невозможно, поскольку выпуклость строго положительна без встроенных опций
- Сумма односторонних длительностей переоценивает длительность. Можно показать, что сумма длительностей двусторонних ключевых ставок занижает общую длительность, но с большей точностью
- Выпуклость в примере преувеличена, чтобы подчеркнуть основные моменты. В действительности влияние на длительность намного меньше, как видно из расчетов в таблице 1
- Добавление дополнительных возможностей, таких как варианты предоплаты, еще больше усложняет ситуацию, поскольку выпуклость может стать отрицательной на некоторых уровнях процентных ставок.Однако главный вывод остается — показатели ключевой ставки, основанные на треугольных сдвигах спотовых ставок, суммируют , а не , как правило, с соответствующей параллельной мерой, а на основе сдвигов, скорректированных влево или вправо, они суммируются!
Влево или вправо? Используйте среднее!
Использование сдвигов с корректировкой влево или вправо — это лучший способ, если вы хотите, чтобы показатели ключевой ставки добавлялись к соответствующим параллельным показателям. Однако выбор между двумя типами смены оказывает значительное влияние на то, как общий риск распределяется по отдельным ключевым ставкам, особенно для выпуклостей.r _ {\ $, i}] $$
, где верхние индексы \ (a \), \ (l \) и \ (r \) соответствуют среднему, левому и правому соответственно. Поскольку обе меры с корректировкой влево и вправо складываются в соответствующую параллельную меру, это также тривиально для метода среднего.
Дельта-векторов
Мы представили, проиллюстрировав дельта-векторы, то есть долларовые дюрации ключевой ставки. Мы рассматриваем односторонний случай для датской государственной облигации без права отзыва 4.5% -2039 (DK00090). Мы используем довольно большой сдвиг в 100 бит / с, чтобы подчеркнуть наши выводы.Дельта-векторы на основе всех четырех методов показаны на рисунке 6.
Рис. 6. Односторонняя долларовая дюрация по ключевой ставке для не подлежащих отзыву государственных облигаций Дании на 4,5% -2039 (DK00090) на основе размера сдвига h = 100 базисных пунктов. Дата расчета — 15 февраля 2018 г., т.е. срок погашения пулевой облигации составляет 21 год.
Пулевые облигации выплачивают фиксированный купон в размере 4,5% годовых и не подлежат отзыву с 21-летним сроком погашения, и поэтому мы ожидаем, что дюрации будут сосредоточены вокруг 20-летней ключевой ставки, что также имеет место.Кроме того, мы наблюдаем, что треугольные сдвиги приводят к наибольшей дюрации ключевой ставки для всех сроков погашения. Это соответствует нашему предыдущему выводу о том, что односторонние треугольные сдвиги спотовой ставки приводят к слишком большой продолжительности.
Крупный платеж при наступлении срока погашения распределяется по-разному по 20-летней и 30-летней ключевым ставкам с использованием метода с корректировкой влево и вправо. Сдвиги с корректировкой влево приписывают большую длительность 20-летней ключевой ставке по сравнению с 30-летней ключевой скоростью по сравнению с методом корректировки вправо.Это наблюдение иллюстрирует основное различие между длительностями ключевой ставки на основе сдвигов, скорректированных влево и вправо.
Опять же, мы выполнили вычисления и представляем вам общие результаты, которые нужно запомнить:
Ключевые результаты по дюрации ключевой ставки
|
Гамма-векторы и выталкивание выпуклости
Мы продолжаем наши иллюстрации с использованием гамма-векторов, то есть выпуклостей по ключевым курсам. Они показаны на рисунке 7 для модели 4.Гособлигации 5% -2039 со сроком смены 10 базисных пунктов.
Рис. 7. Выпуклость ключевой процентной ставки по безотзывной государственной пулевой облигации Дании на 4,5% -2039 (DK00090) на основе размера сдвига h = 10 базисных пунктов. Дата расчета — 15 февраля 2018 г., т.е. срок погашения пулевой облигации составляет 21 год.
Из примера видно, что выпуклость ключевой процентной ставки в долларах, основанная на треугольных сдвигах, как правило, ниже по сравнению с значениями, скорректированными влево и вправо.Это естественное следствие того факта, что сумма треугольных выпуклостей доллара по ключевой ставке всегда меньше, чем выпуклость доллара, тогда как выпуклости доллара с поправкой на левую и правую стороны складываются.
Кроме того, метод с корректировкой влево придает большую выпуклость 30-летнему сроку погашения по сравнению с методом с корректировкой вправо и, наоборот, для срока погашения с ключевой ставкой 20 лет. Это явление связано с смещением выпуклостей ключевой ставки, которое является общим для необслуживаемых облигаций при применении сдвигов, скорректированных влево и вправо:
Ключевые результаты для выпуклостей ключевой ставки
|
Чтобы проиллюстрировать стремление к выпуклости, рассмотрим бескупонную облигацию со сроком погашения, расположенным точно посередине между двумя сроками погашения ключевой ставки.Сдвиги с корректировкой влево будут приписывать только ¼ выпуклости левой ключевой скорости, оставляя ¾ выпуклости правой ключевой скорости. И наоборот, для сдвигов, отрегулированных вправо. Метод среднего значения будет относить 1/2 выпуклости к каждой из двух ключевых ставок.
Что нужно запомнить
В этом блоге мы описываем классические меры риска, такие как дюрация и выпуклость, и то, как они соотносятся с их аналогами по ключевой ставке. Наши основные выводы:
Обобщение основных результатов
|
Сноски:
1 Длительность ключевой ставки: показатели процентных рисков, Томас Хо, Журнал фиксированного дохода, сентябрь 1992 г., стр.29-44.
2 Для облигаций без встроенной опционности это просто численные аппроксимации классической долларовой дюрации и выпуклости при применении параллельного сдвига. Если облигация имеет встроенную опциональность, например если это датская облигация с отзывным ипотечным покрытием с возможностью досрочного погашения, наши меры являются версиями с корректировкой по опциону.
3 Формулы продолжительности и выпуклости для сдвигов, скорректированных влево, аналогичны, просто замените \ (i + 1 \) на \ (i — 1 \).Обратите внимание, что \ (P (s_0 (h)) = P_i \) , поскольку мы начинаем слева, используя несмещенную кривую.
PM2059 Регулировка продолжительности ключевой ставки_v3.indd
% PDF-1.3
%
1 0 объект
>] / PageLabels 6 0 R / Pages 3 0 R / Type / Catalog / ViewerPreferences >>>
эндобдж
2 0 obj
> поток
2017-01-25T10: 01: 07-06: 002017-01-25T10: 01: 13-06: 002017-01-25T10: 01: 13-06: 00 Adobe InDesign CC 2015 (Macintosh) uuid: 5de58c0e-5217-5647 -8f73-5a2270dfbff9xmp.did: 0A80117407206811AB08C5C8D3B74040xmp.ID: d94ea8dc-d288-4381-a161-0dc6f8f9b185proof: pdf1xmp.iid: 56a5b41b-549f-47bf-bff9-abd278d2a219xmp.did: 8ee18fc1-6648-4cc2-993f-9a6d8c331d1cxmp.did: 0A80117407206811AB08C5C8D3B74040default
application / pdf
Библиотека Adobe PDF 15.0FalsePDF / X-1: 2001PDF / X-1: 2001PDF / X-1a: 2001
конечный поток
эндобдж
6 0 obj
>
эндобдж
3 0 obj
>
эндобдж
9 0 объект
>
эндобдж
10 0 obj
>
эндобдж
16 0 объект
> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [0.0 0,0 612,0 792,0] / Тип / Страница >>
эндобдж
17 0 объект
> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [0.0 0.0 612.0 792.0] / Type / Page >>
эндобдж
18 0 объект
> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [0.0 0.0 612.0 792.0] / Type / Page >>
эндобдж
19 0 объект
> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [0.0 0.0 612.0 792.0] / Type / Page >>
эндобдж
20 0 объект
> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [0.> xo, pxFO ה x’fX`ub @ / h2% \ Vw 氳 ~ v ׃ cig`, @@ {Z؟ JP: bd8Iƾl 悋 FOZ, Q; NͤDFr @ $ KEȰWHKꘊpPo`M} jH +; ‘nkI, + \ ~ Hdd˦:,? ڗ I
Понимание риска и доходности фиксированного дохода
Этот показатель охватывает характеристики риска и доходности облигаций с фиксированной процентной ставкой. Основное внимание уделяется широко используемым показателям процентного риска — дюрации и выпуклости. Эти статистические данные широко используются при анализе фиксированного дохода. Ниже приведены основные моменты, сделанные при чтении:
Три источника дохода по облигации с фиксированной процентной ставкой, купленной по номинальной стоимости: (1) получение обещанных купонных выплат и основной суммы в запланированные даты, (2) реинвестирование купонных выплат и (3) потенциальный прирост капитала а также убытки от продажи облигации до погашения.
Для облигации, купленной с дисконтом или премией, норма доходности также включает эффект «подтягивания к номинальной стоимости» по мере приближения срока погашения, при условии отсутствия дефолта.
Общий доход — это будущая стоимость реинвестированных выплат по купонному вознаграждению и цена продажи (или погашение основной суммы, если облигация удерживается до погашения).
Горизонтальная доходность (или норма доходности периода владения) — это внутренняя норма доходности между общей доходностью и покупной ценой облигации.
Риск реинвестирования купона увеличивается с увеличением купонной ставки и более длительным периодом реинвестирования.
Прирост капитала и убытки измеряются по балансовой стоимости облигации, а не по цене покупки. Балансовая стоимость включает амортизацию дисконта или премии, если облигация приобретается по цене ниже или выше номинальной стоимости. Балансовая стоимость — это любая точка на траектории постоянной доходности.
Процентный доход по облигации — это доход, связанный с течением времени.Прирост капитала и убыток — это доходность, связанная с изменением стоимости облигации, на что указывает изменение доходности к погашению.
Два типа процентного риска по облигации с фиксированной ставкой — это риск реинвестирования купона и риск рыночной цены. Эти риски в определенной степени компенсируют друг друга. Инвестор получает прибыль от более высоких ставок по реинвестированным купонам, но проигрывает, если облигация продается с убытком капитала, потому что цена ниже траектории постоянной доходности.Инвестор проигрывает из-за более низких ставок по реинвестированному купону, но получает прибыль, если облигация продается с приростом капитала, потому что цена выше траектории постоянной доходности.
Риск рыночной цены преобладает над риском реинвестирования купона, когда у инвестора краткосрочный горизонт (относительно времени до погашения облигации).
Риск реинвестирования купона преобладает над риском рыночной цены, когда у инвестора есть долгосрочный горизонт (относительно времени до погашения) — например, инвестор «покупай и держи».
Дюрация облигации, как правило, измеряет чувствительность полной цены (включая начисленные проценты) к изменению процентных ставок.
Статистика дюрации доходности, измеряющая чувствительность полной цены облигации к ее собственной доходности к погашению, включает дюрацию Маколея, модифицированную дюрацию, денежную дюрацию и ценовую стоимость базисного пункта.
Кривая статистики дюрации, измеряющая чувствительность полной цены облигации к эталонной кривой доходности, обычно называется «эффективной дюрацией».”
Дюрация Маколея — это средневзвешенное время до получения купонных выплат по процентам и основной сумме, в котором веса являются долями полной цены, соответствующей каждому платежу. Эта статистика рассчитывается путем деления на периодичность (количество купонных выплат или периодов начисления сложных процентов в году).
Модифицированная дюрация обеспечивает линейную оценку процентного изменения цены облигации с учетом изменения ее доходности к погашению.
Приблизительная модифицированная дюрация приближается к модифицированной дюрации, поскольку изменение доходности к погашению приближается к нулю.
Эффективная продолжительность очень похожа на приблизительную модифицированную продолжительность. Разница в том, что приблизительная модифицированная дюрация — это статистика дюрации доходности, которая измеряет риск процентной ставки с точки зрения изменения собственной доходности к погашению, тогда как эффективная дюрация — это статистика продолжительности кривой, которая измеряет риск процентной ставки, предполагая параллельный сдвиг в эталонная кривая доходности.
Дюрация ключевой ставки — это мера чувствительности облигации к изменению базовой кривой доходности на определенных сегментах срока погашения. Дюрация ключевой ставки может использоваться для измерения чувствительности облигации к изменениям формы кривой доходности.
Облигации со встроенным опционом не имеют значимой внутренней нормы доходности, поскольку будущие денежные потоки зависят от процентных ставок. Следовательно, эффективная дюрация является подходящей мерой процентного риска, а не модифицированной дюрацией.
Эффективная дюрация традиционной (безопционной) облигации с фиксированной ставкой — это ее чувствительность к эталонной кривой доходности, которая может отличаться от ее чувствительности к собственной доходности к погашению. Следовательно, модифицированная дюрация и эффективная дюрация традиционной (безопционной) облигации с фиксированной ставкой не обязательно равны.
В течение купонного периода дюрации Маколея и модифицированные дюрации плавно снижаются по «пилообразной» схеме, при условии, что доходность к погашению является постоянной.После выплаты купона продолжительность увеличивается.
Дюрация Маколея и модифицированная дюрация обратно пропорциональны ставке купона и доходности к погашению.
Срок до погашения, дюрация Маколея и модифицированная дюрация обычно положительно связаны с . Их всегда положительно связаны с облигациями с номинальной стоимостью или с премией выше номинальной. Это , как правило, , положительно связанных с облигациями, оцененными с дисконтом ниже номинальной стоимости.Исключение составляют долгосрочные облигации с низким купоном, дюрация которых может быть меньше, чем у сопоставимых в остальном более краткосрочных облигаций.
Наличие встроенного опциона на покупку снижает эффективную дюрацию облигации по сравнению с дюрацией сопоставимой в иных отношениях облигации без права отзыва. Снижение эффективной дюрации больше, когда процентные ставки низкие и эмитент с большей вероятностью исполнит колл-опцион.
Наличие встроенного опциона на продажу снижает эффективную дюрацию облигации по сравнению с дюрацией другой сопоставимой облигации без права обратной продажи.Снижение эффективной дюрации больше, когда процентные ставки высоки и инвестор с большей вероятностью исполнит пут-опцион.
Дюрация портфеля облигаций может быть рассчитана двумя способами: (1) средневзвешенное время до получения совокупных денежных потоков и (2) средневзвешенное значение дюрации отдельных облигаций, составляющих портфель.
Первый метод расчета дюрации портфеля основан на доходности денежного потока, которая представляет собой внутреннюю норму доходности совокупных денежных потоков.Его нельзя использовать для облигаций со встроенными опционами или для нот с плавающей ставкой.
Второй метод проще в использовании и достаточно точен, когда кривая доходности относительно плоская. Его главное ограничение заключается в том, что он предполагает параллельный сдвиг кривой доходности, так как доходность всех облигаций в портфеле изменяется на одинаковую величину.
Дюрация денег — это мера изменения цены в единицах валюты, в которой номинирована облигация.
Ценовая стоимость базисного пункта (PVBP) — это оценка изменения полной цены облигации при изменении доходности к погашению на 1 б.п.
Модифицированная дюрация — это первичный эффект первого порядка на процентное изменение цены облигации с учетом изменения доходности к погашению. Выпуклость — это вторичный эффект, или эффект второго порядка. Он указывает на изменение модифицированной дюрации по мере изменения доходности к погашению.
Выпуклость денег — это выпуклость, умноженная на полную стоимость облигации.В сочетании с дюрацией денег, выпуклость денег оценивает изменение полной цены облигации в денежных единицах с учетом изменения доходности к погашению.
Выпуклость — положительный атрибут облигации. При прочих равных условиях более выпуклая облигация дорожает больше, чем менее выпуклая облигация, когда доходность падает, и меньше обесценивается, когда доходность растет.
Эффективная выпуклость — это эффект второго порядка на цену облигации при изменении эталонной кривой доходности.Это похоже на приблизительную выпуклость. Разница в том, что приблизительная выпуклость основана на изменении доходности к погашению, а эффективная выпуклость основана на изменении базовой кривой доходности.
Облигации с правом отзыва имеют отрицательную эффективную выпуклость при низких процентных ставках. Увеличение цены при снижении эталонной доходности по абсолютной величине меньше, чем снижение цены при повышении эталонной доходности.
Изменение цены облигации является продуктом: (1) воздействия на изменение доходности к погашению на базисный пункт и (2) количества базисных пунктов в изменении доходности.Первый фактор оценивается по длительности и выпуклости. Второй фактор зависит от волатильности доходности.
Инвестиционный горизонт важен для измерения процентного риска по облигации с фиксированной процентной ставкой.
Для конкретного допущения о волатильности доходности дюрация Маколея указывает инвестиционный горизонт, для которого риск реинвестирования купона и риск рыночной цены уравновешивают друг друга. Допущение заключается в однократном параллельном сдвиге кривой доходности, при которой доходность к погашению и ставка реинвестирования купона изменяются на одну и ту же величину в одном и том же направлении.
Когда инвестиционный горизонт превышает дюрацию Маколея по облигации, риск реинвестирования купона преобладает над ценовым риском. Риск инвестора заключается в снижении процентных ставок. Разрыв в продолжительности отрицательный.
Когда инвестиционный горизонт равен дюрации Маколея по облигации, риск реинвестирования купона компенсирует ценовой риск. Разрыв в продолжительности равен нулю.