Что такое процент годовых: Как начисляются проценты по кредиту? | КонсультантПлюс
Как жители стран мира сохраняют сбережения во время коронакризиса — Российская газета
Американцы отличаются довольно высоким уровнем финансовой грамотности и охотно экспериментируют с разными формами инвестиций. Это особенно наглядно проявляется в кризисные времена, такие как этот терзаемый пандемией коронавируса год. Согласно статистике министерства торговли США, весной американцы радикально уменьшили текущие расходы и откладывали на сбережения рекордные 33 процента своих доходов. К лету этот показатель снизился до 19 процентов, что все равно намного выше среднего уровня последних лет около 6-7 процентов.
Инвестиционный портфель принято составлять из нескольких инструментов. Если говорить о популярных в нашей стране вкладах, то а Америке ставки по таким продуктам невелики. Например, типичная доходность по депозитам в основных банках не превышает 0,6-0,8 процента годовых. Что касается сберегательных счетов, то прибыль по ним и вовсе символическая — от 0,05 процента годовых. Помимо ликвидности их плюс по сравнению с более доходными и рискованными активами в том, что все накопления на таких счетах застрахованы государством на сумму до 250 тысяч долларов. В специальных кредитных объединениях ставки несколько выше, чем в банках, но все равно не превышают примерно 1,5 процента годовых даже по долгосрочным вложениям (на 5 лет). Поэтому такие депозиты считаются скорее средством сохранения сбережений, чем их приумножения. Вклады и сберегательные счета — лишь третий по популярности в США тип инвестирования накоплений. По данным финансового аналитического ресурса Bankrate, на первое место такой инструмент ставят примерно 19 процентов американцев.
В США отдают предпочтение долгосрочным инвестициям. Фаворитом среди них долгое время являлись ценные бумаги. Например, вложения в фонд акций по индексу Standard & Poor s 500 в среднем на протяжении последних десятилетий стабильно приносили доход около 10 процентов годовых. Такие инвестиции для большинства считаются долгосрочными (от 3-5 лет), поскольку на короткий срок из-за волатильности финансовых рынков они могут быть и убыточными.
Но в последние пару лет восстанавливающаяся после краха в конце прошлого десятилетия недвижимость серьезно потеснила позиции ценных бумаг. Согласно опросам социологов, примерно треть американцев, отвечая на вопрос о том, куда бы они вложили сбережения, которые не пригодятся им в ближайшие 10 или более лет, выбрали бы именно покупку недвижимости.
Доходность по вкладам в США не превышает 0,8 процента годовых, поэтому для приумножения накоплений американцы приобретают акции
Определенную популярность имеют драгметаллы, которым отдает приоритет каждый десятый американец. Криптовалюты и другие экзотические вложения считают лучшей инвестицией менее 5 процентов.
Особое место в портфеле инвестиций занимают индивидуальные пенсионные счета, которые американцы стараются открыть уже в молодости ради накоплений на безбедную старость. Сами по себе дохода они не приносят, но зато на отчисления в них пользуются налоговыми льготами. С учетом того, что налоговые ставки в США довольно высоки (от 10 до 37 процентов в зависимости от суммы доходов), уже одно это делает такие планы неплохой инвестицией. Кроме того, размещенные на таком счету средства можно дополнительно вкладывать как в депозиты, так и в ценные бумаги с тем, чтобы увеличить сумму накоплений. Следует только учитывать, что средства на таком счете, как правило, заморожены на десятилетия и воспользоваться ими получится лишь по выходу на пенсию. Многим такие пенсионные планы предоставляет работодатель, но примерно каждый третий американец, работающий в частном секторе, не имеет этой опции в своем контракте.
Вклад «Проценты вперед» — банковские услуги юридическим и частным лицам
Правовая информация
Условия использования данного интернет-сайта
Указанные ниже условия определяют порядок использования данного интернет-сайта. Пользуясь доступом к этому интернет-сайту (в том числе к любой из его страниц) Вы, тем самым, соглашаетесь соблюдать изложенные ниже условия в полной мере.
Обращаем Ваше внимание, что если Вы уже являетесь клиентом ООО «Экспобанк», то настоящие условия следует применять совместно с положениями и требованиями, определенными в соответствующем договоре между Вами и ООО «Экспобанк». Просим принять во внимание, что все продукты и услуги ООО «Экспобанк» предоставляются Вам на основании соответствующих договоров.
ООО «Экспобанк» оставляет за собой право изменить настоящие условия в любое время без предварительного уведомления пользователей данного интернет-сайта путем внесения необходимых изменений в настоящие условия. Продолжая использовать доступ к данному интернет-сайту (в том числе к любой из его страниц) Вы, тем самым, подтверждаете Ваше согласие соблюдать все изменения в настоящих условиях.
Доступ к сайту
ООО «Экспобанк» имеет право по своему усмотрению в одностороннем порядке ограничить доступ к информации, содержащейся на данном интернет-сайте, в том числе (но, не ограничиваясь) если есть основания полагать, что такой доступ осуществляется с нарушением настоящих условий.
Обращаем Ваше внимание, что данный интернет-сайт разработан таким образом, и его структура подразумевает, что доступ к интернет-сайту и получение соответствующей информации должны начинаться со стартовой страницы интернет-сайта. В этой связи, доступ к любой странице этого интернет-сайта посредством прямой ссылки на такую страницу, минуя стартовую страницу данного интернет-сайта может означать, что Вы не увидите важную информацию о данном интернет-сайте, а также условия использования этого интернет-сайта.
Авторские права
Информация, содержащаяся на данном интернет-сайте, предназначена только для Вашего личного использования. Запрещается сохранять, воспроизводить, передавать или изменять любую часть данного интернет-сайта без предварительного письменного разрешения ООО «Экспобанк». Разрешается распечатка информации с данного интернет-сайта только для Вашего личного использования такой информации.
Разрешается распечатка информации с данного интернет-сайта только для Вашего личного использования такой информации.
Продукты и услуги третьих лиц
В случае если на данном интернет-сайте находятся ссылки на интернет-сайты третьих лиц, такие ссылки не являются поддержкой, продвижением, либо рекламой со стороны ООО «Экспобанк» продуктов или услуг предлагаемых на таких интернет-сайтах третьих лиц. Вы самостоятельно несете всю ответственность, связанную с использованием Вами указанных ссылок для доступа к интернет-сайтам третьих лиц. ООО «Экспобанк» не несет ответственности или обязанности за содержание, использование или доступность таких интернет-сайтов третьих лиц или за любые потери или ущерб, возникающие в результате использования таких интернет-сайтов третьих лиц. ООО «Экспобанк» не проверяет, не гарантирует и не несет ответственности за точность и корректность информации, содержащейся на таких интернет-сайтах третьих лиц.
Данный интернет-сайт может содержать материалы и информацию, предоставленные третьими лицами. ООО «Экспобанк» не несет ответственности или обязанности за точность и корректность таких материалов и информации.
Третьим лицам запрещается размещать ссылки на данный интернет-сайт в других интернет-сайтах или размещать ссылки в данном интернет-сайте на другие интернет-сайты без предварительного получения письменного согласия ООО «Экспобанк».
Отсутствие оферты
Никакая информация, содержащаяся на данном интернет-сайте, не может и не должна рассматриваться в качестве предложения или рекомендации о приобретении или размещении любых инвестиций или о заключении любой другой сделки или предоставлении инвестиционных советов или оказании услуг.
Отсутствие гарантий
Принимая во внимание, что ООО «Экспобанк» предпринимает и будет предпринимать все разумные меры для обеспечения аккуратности и достоверности информации размещенной на данном интернет-сайте, следует учитывать, что ООО «Экспобанк» не гарантирует и не принимает никаких обязательств (прямых и косвенных) по отношению к точности, своевременности и полноте размещенной на данном интернет-сайте информации.
Оценки, заключения и любая другая информация, размещенные на данном интернет-сайте следует применять только в информационных целях и только для Вашего персонального использования (принимая во внимание порядок изменения настоящих условий, изложенный в начале).
Никакая информация, размещенная на данном интернет-сайте, не может и не должна рассматриваться в качестве инвестиционного, юридического, налогового или любого другого совета или консультации, и не предназначена и не должна использоваться при принятии каких-либо решений (в том числе инвестиционных). Вам следует получить соответствующую специфическую профессиональную консультацию, прежде чем принять какое-либо решение (в том числе инвестиционное).
Ограничение ответственности
ООО «Экспобанк» ни при каких обстоятельствах не несет ответственности или обязательств ни за какой ущерб, включая (без ограничений) ущерб или потери любого вида вследствие невнимательности, включая (без ограничений) прямые, косвенные, случайные, специальные или сопутствующие убытки, ущерб или расходы, возникшие в связи с данным интернет-сайтом, его использованием, доступом к нему, или невозможностью использования или связанные с любой ошибкой, несрабатыванием, неисправностью, компьютерным вирусом или сбоем оборудования, или потеря дохода или деловой репутации, даже в тех случаях, когда в явно выраженной форме Вам было сообщено о возможности таких потерь или ущерба, возникших в связи доступом, использованием, работой, просмотром данного интернет-сайта, или размещенных на данном интернет-сайте ссылок на интернет-сайты третьих лиц.
ООО «Экспобанк» оставляет за собой право изменять, приостанавливать или прекращать временно или на постоянной основе работу данного интернет-сайта или любой его части с предварительным уведомлением или без предварительного уведомления в любое время по своему усмотрению. Вы подтверждаете и соглашаетесь, что все изменения, приостановление или прекращение работы данного интернет-сайта не влекут возникновения каких-либо обязательств перед Вами со стороны ООО «Экспобанк».
Регулирующее законодательство
Настоящие условия регулируются законодательством Российской Федерации. Вы подтверждаете и соглашаетесь, что все вопросы и споры, возникающие в связи с данным интернет-сайтом и условиями его использования подлежат рассмотрению в юрисдикции Российской Федерации.
Данный интернет-сайт разработан для использования в Российской Федерации и не предназначен для использования любым физическим или юридическим лицом, находящимся в юрисдикции или стране, где публикация информации, размещенной на данном интернет-сайте или возможность доступа к данному интернет-сайту или распространение информации с помощью данного интернет-сайта или иное использование данного интернет-сайта нарушают законодательство такой юрисдикции или страны. В случае если Вы решили воспользоваться доступом к информации, размещенной на данном интернет-сайте, обращаем Ваше внимание, что Вы самостоятельно несете ответственность за соблюдение применимых местных, государственных или международных законов, и Вы самостоятельно несете ответственность за любое использование информации размещенной на данном интернет-сайте вне юрисдикции Российской Федерации. В случае возникновения какого-либо вопроса, связанного с применением регулирующего законодательства, рекомендуем Вам обратиться за помощью к Вашему консультанту по юридическим вопросам.
Вклад «Доходный» с высокими процентными ставками до 8,5% в Россельхозбанке 2020 в рублях и валюте
А
Адыгейский
Алтайский
Амурский
Архангельский
Б
Башкирский
Белгородский
Брянский
Бурятский
В
Владимирский
Волгоградский
Воронежский
Д
Дагестанский
И
Ивановский
Ингушский
Иркутский
К
Кабардино-Балкарский
Калининградский
Калужский
Камчатский
Кемеровский
Кировский
Коми
Костромской
Краснодарский
Красноярский
Курский
Л
Липецкий
М
Марийский
Мордовский
Московский ЦРМБ
Н
Нижегородский
Новгородский
Новосибирский
О
Омский
Оренбургский
Орловский
П
Пензенский
Пермский
Приморский
Псковский
Р
Ростовский
Рязанский
С
Самарский
Санкт-Петербургский
Саратовский
Сахалинский
Свердловский
Смоленский
Ставропольский
Т
Тамбовский
Татарстанский
Тверской
Томский
Тувинский
Тульский
Тюменский
У
Удмуртский
Ульяновский
Х
Хабаровский
Ц
Центр корпоративного бизнеса
Ч
Челябинский
Чеченский
Читинский
Простой калькулятор процентов — WebMath
Быстро! Мне нужна помощь с:
Выберите элемент справки по математике . .. Исчисление, Производное вычисление, Интеграционное вычисление, Частное правило, Монеты, Подсчет комбинаций, Поиск всех сложных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование площади, Преобразование длины, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, The Equation from slopeLinesLines Theotation, The Equation from slopeLines Theotation и Y-intation , Нахождение шансовМатематика, Практика многочленов по математике, Практика основМетрическая система, Преобразование чисел, Сложение чисел, Вычисление с числами, Вычисление с переменными числами, Деление чисел, Умножение чисел, Сравнение числовых линий, Числовые строки, Разместите значения чисел, Произношение чисел, Округление чисел, Вычитание числа слагаемых, Вычитание числа Квадратные многочлены, Деление многочленов, Факторизация разности квадратов многочленов, Факторизация триномов многочленов, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они представляют собой Устранение, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, УмножениеФормы, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение продуктов , Правые треугольники, Ветер, Рисунок
.. Исчисление, Производное вычисление, Интеграционное вычисление, Частное правило, Монеты, Подсчет комбинаций, Поиск всех сложных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование площади, Преобразование длины, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, The Equation from slopeLinesLines Theotation, The Equation from slopeLines Theotation и Y-intation , Нахождение шансовМатематика, Практика многочленов по математике, Практика основМетрическая система, Преобразование чисел, Сложение чисел, Вычисление с числами, Вычисление с переменными числами, Деление чисел, Умножение чисел, Сравнение числовых линий, Числовые строки, Разместите значения чисел, Произношение чисел, Округление чисел, Вычитание числа слагаемых, Вычитание числа Квадратные многочлены, Деление многочленов, Факторизация разности квадратов многочленов, Факторизация триномов многочленов, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они представляют собой Устранение, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, УмножениеФормы, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение продуктов , Правые треугольники, Ветер, Рисунок
Как рассчитать ежемесячные проценты
Ежемесячный расчет процентов — важный навык. Вы часто видите процентные ставки, выраженные в процентах в годовом исчислении — либо годовой процентной доходности (APY), либо годовой процентной ставки (APR), — но полезно точно знать, сколько это в сумме в долларах и центах. Обычно мы думаем о ежемесячных расходах.
Вы часто видите процентные ставки, выраженные в процентах в годовом исчислении — либо годовой процентной доходности (APY), либо годовой процентной ставки (APR), — но полезно точно знать, сколько это в сумме в долларах и центах. Обычно мы думаем о ежемесячных расходах.
Например, у вас есть ежемесячные счета за коммунальные услуги, расходы на питание или оплату автомобиля. Проценты также являются ежемесячным (если не ежедневным) событием, и эти повторяющиеся расчеты процентов составляют большие числа в течение года. Выплачиваете ли вы проценты по ссуде или получаете проценты на сберегательном счете, процесс перехода с годовой ставки (APY или APR) на ежемесячную процентную ставку одинаков.
Пример расчета месячной процентной ставки
Чтобы рассчитать ежемесячную процентную ставку, разделите годовую ставку на 12, чтобы отразить 12 месяцев в году. Вам нужно будет преобразовать процентное значение в десятичный формат, чтобы выполнить эти шаги.
Пример: Предположим, ваша APY или годовая процентная ставка составляет 10%. Какова ваша ежемесячная процентная ставка и сколько вы бы заплатили или заработали на 2000 долларов?
- Преобразуйте годовую ставку из процента в десятичную дробь, разделив на 100: 10/100 = 0.10
- Теперь разделите это число на 12, чтобы получить ежемесячную процентную ставку в десятичной форме: 0,10 / 12 = 0,0083
- Чтобы рассчитать ежемесячные проценты по 2000 долларов, умножьте это число на общую сумму: 0,0083 x 2000 долларов = 16,60 долларов в месяц
- Преобразуйте месячную ставку в десятичном формате обратно в проценты (умножив на 100): 0,0083 x 100 = 0,83%
- Ваша ежемесячная процентная ставка 0,83%
Хотите, чтобы вам была заполнена таблица с этим примером? См. Бесплатную таблицу «Пример ежемесячных процентов» и сделайте копию таблицы, чтобы использовать ее со своими числами.Приведенный выше пример является самым простым способом расчета ежемесячных процентных ставок и стоит за один месяц .
Вы можете рассчитывать проценты за месяцы, дни, годы или любой другой период. Какой бы период вы ни выбрали, ставка, которую вы используете в расчетах, называется периодической процентной ставкой. Чаще всего вы будете видеть ставки, выраженные в годовом исчислении, поэтому вам обычно нужно переходить на любую периодическую ставку, соответствующую вашему вопросу или вашему финансовому продукту.
Вы можете использовать ту же концепцию расчета процентной ставки с другими периодами времени:
- Для ежедневной процентной ставки разделите годовую ставку на 360 (или 365, в зависимости от вашего банка).
- Для квартальной ставки разделите годовую ставку на четыре.
- Для недельной ставки разделите годовую ставку на 52.
Амортизация
При большом количестве ссуд остаток по кредиту меняется каждый месяц. Например, по автокредитам, жилищным и личным кредитам вы постепенно выплачиваете свой баланс с течением времени и, как правило, каждый месяц получаете меньший баланс.
Этот процесс называется амортизацией, и таблица амортизации помогает вам рассчитать (и показывает) точно, сколько процентов вы платите каждый месяц.
Со временем ваши ежемесячные процентные расходы уменьшаются — и сумма, которая идет на остаток по ссуде , увеличивается на .
Жилищные ссуды и кредитные карты
Ипотечные кредиты могут быть сложными. Разумно использовать график погашения, чтобы понять ваши процентные расходы, но вам может потребоваться дополнительная работа, чтобы определить вашу фактическую ставку. Вы можете знать годовую процентную ставку (APR) по ипотечному кредиту, но APR может содержать дополнительные расходы помимо процентов (например, расходы на закрытие).Также может измениться ставка по ипотеке с регулируемой процентной ставкой.
С кредитными картами вы можете добавлять новые платежи и погашать задолженность несколько раз в течение месяца. Все это делает расчеты более громоздкими, но все же стоит знать, как складываются ваши ежемесячные проценты. Во многих случаях вы можете использовать средний дневной баланс, который представляет собой сумму баланса за каждый день, разделенную на количество дней в каждом месяце (а финансовые расходы рассчитываются с использованием среднего дневного баланса).В других случаях эмитент вашей карты взимает проценты ежедневно (поэтому вам нужно рассчитывать дневную процентную ставку, а не ежемесячную).
Во многих случаях вы можете использовать средний дневной баланс, который представляет собой сумму баланса за каждый день, разделенную на количество дней в каждом месяце (а финансовые расходы рассчитываются с использованием среднего дневного баланса).В других случаях эмитент вашей карты взимает проценты ежедневно (поэтому вам нужно рассчитывать дневную процентную ставку, а не ежемесячную).
Процентные ставки и годовая процентная ставка
Обязательно используйте в своих расчетах процентную ставку , а не годовую процентную доходность.
APY учитывает сложное начисление, то есть проценты, которые вы зарабатываете по мере роста вашего счета за счет выплаты процентов. APY будет выше, чем ваша фактическая ставка, если проценты не начисляются ежегодно, поэтому APY может дать неточный результат.Тем не менее, APY позволяет быстро узнать, сколько вы будете зарабатывать ежегодно на сберегательном счете, без пополнений или снятия средств.
Простой процент против сложного процента
Простой процент против сложного процента: обзор
Проценты — это стоимость заимствования денег, когда заемщик платит кредитору комиссию за ссуду. Проценты, обычно выражаемые в процентах, могут быть простыми или сложными. Простой процент основан на основной сумме кредита или депозита.Напротив, сложные проценты основаны на основной сумме и процентах, которые накапливаются по ней за каждый период. Простые проценты начисляются только на основную сумму ссуды или депозита, поэтому их легче определить, чем сложные проценты.
Ключевые выводы
- Проценты — это стоимость заимствования денег, когда заемщик платит кредитору комиссию за ссуду.
- Как правило, простые проценты, выплачиваемые или полученные в течение определенного периода, представляют собой фиксированный процент от основной суммы, которая была заимствована или предоставлена в ссуду.
- Сложные проценты начисляются и добавляются к накопленным процентам за предыдущие периоды, поэтому заемщики должны уплачивать проценты по процентам, а также основную сумму долга.

Разница между сложным процентом и простым процентом
Простые проценты
Простой процент рассчитывается по следующей формуле:
Взаимодействие с другими людьми
Простой интерес
знак равно
п
×
р
×
п
куда:
п
знак равно
Основная сумма
р
знак равно
Годовая процентная ставка
п
знак равно
Срок кредита, лет
\ begin {align} & \ text {Simple Interest} = P \ times r \ times n \\ & \ textbf {где:} \\ & P = \ text {Основная сумма} \\ & r = \ text {Годовая процентная ставка} \\ & n = \ text {Срок кредита в годах} \\ \ end {выравнивается}
Простой процент = P × r × n, где: P = основная сумма r = годовая процентная ставка = срок кредита в годах
Как правило, простые проценты, выплачиваемые или полученные в течение определенного периода, представляют собой фиксированный процент от основной суммы, которая была заимствована или ссужена.Например, предположим, что студент получает ссуду с простой процентной ставкой для оплаты одного года обучения в колледже, которое стоит 18000 долларов, а годовая процентная ставка по ссуде составляет 6%. Студент погашает ссуду в течение трех лет. Выплачиваемая сумма простых процентов составляет:
Взаимодействие с другими людьми
$
3
,
2
4
0
знак равно
$
1
8
,
0
0
0
×
0
.
0
6
×
3
\ begin {align} & \ $ 3,240 = \ 18 000 $ \ times 0,06 \ times 3 \\ \ end {align}
3240 долларов = 18000 долларов × 0,06 × 3
а общая выплаченная сумма составляет:
Взаимодействие с другими людьми
$
2
1
,
2
4
0
знак равно
$
1
8
,
0
0
0
+
$
3
,
2
4
0
\ begin {align} & \ 21 240 долларов = \ 18 000 долларов США + \ 3 240 долларов США \\ \ end {align}
21 240 долл. США = 18 000 долл. США + 3 240 долл. США
Сложные проценты
Сложные проценты начисляются и добавляются к накопленным процентам за предыдущие периоды; Другими словами, он включает проценты по процентам.t — P \\ & \ textbf {где:} \\ & P = \ text {Основная сумма} \\ & r = \ text {Годовая процентная ставка} \\ & t = \ text {Применяется процентная ставка за количество лет} \\ \ конец {выровнен}
Сложные проценты = P × (1 + r) t − P, где: P = основная сумма r = годовая процентная ставка t = количество лет, на которые начисляются проценты
Он рассчитывается путем умножения основной суммы на единицу плюс годовая процентная ставка, повышенная на количество сложных периодов, а затем минус уменьшение основной суммы за этот год. В случае сложных процентов заемщики должны выплачивать проценты как на проценты, так и на основную сумму.
В случае сложных процентов заемщики должны выплачивать проценты как на проценты, так и на основную сумму.
Примеры простых и сложных процентов
Ниже приведены несколько примеров простых и сложных процентов.
Пример 1
Предположим, вы вложили 5000 долларов в годовой депозитный сертификат (CD), по которому выплачиваются простые проценты под 3% годовых. Процент, который вы заработаете через год, составит 150 долларов:
Взаимодействие с другими людьми
$
5
,
0
0
0
×
3
%
×
1
\ begin {выровнено} & \ 5 000 $ \ times 3 \% \ times 1 \\ \ end {выровнено}
5000 долларов США × 3% × 1
Пример 2
Продолжая приведенный выше пример, предположим, что ваш депозитный сертификат можно обналичить в любое время, а проценты выплачиваются вам пропорционально.Если вы обналичите компакт-диск через четыре месяца, сколько вы заработаете в виде процентов? Вы получите 50 долларов:
$
5
,
0
0
0
×
3
%
×
4
1
2
\ begin {align} & \ $ 5,000 \ times 3 \% \ times \ frac {4} {12} \\ \ end {align}
5000 долларов США × 3% × 124
Пример 3
Предположим, Боб занимает 500 000 долларов на три года у своего богатого дяди, который соглашается взимать с Боба простые проценты под 5% годовых. Сколько Бобу придется выплачивать проценты каждый год и каковы будут его общие проценты через три года? (Предположим, что основная сумма остается неизменной в течение трех лет, т.е.д., полная сумма кредита будет выплачена через три года.) Бобу придется платить 25000 долларов в качестве процентов каждый год:
Взаимодействие с другими людьми
$
5
0
0
,
0
0
0
×
5
%
×
1
\ begin {выровнен} & \ 500 000 $ \ times 5 \% \ times 1 \\ \ end {выровнен}
500 000 долларов США × 5% × 1
или 75 000 долларов США в виде процентов по истечении трех лет:
Взаимодействие с другими людьми
$
2
5
,
0
0
0
×
3
\ начало {выровнено} & \ 25 000 $ \ times 3 \\ \ end {выровнено}
25 000 долл. США × 3
США × 3
Пример 4
Продолжая приведенный выше пример, Бобу необходимо дополнительно занять 500 000 долларов на три года.К сожалению, его богатый дядя отключен. Таким образом, он берет ссуду в банке по процентной ставке 5% годовых, начисляемых ежегодно, с выплатой полной суммы ссуды и процентов через три года. Каков будет общий процент, выплачиваемый Бобом?
Поскольку сложные проценты рассчитываются на основе основной суммы и накопленных процентов, вот как они складываются:
Взаимодействие с другими людьми
После первого года выплаты процентов
знак равно
$
2
5
,
0
0
0
,
или же
$
5
0
0
,
0
0
0
(Основная сумма займа)
×
5
%
×
1
После второго года выплата процентов
знак равно
$
2
6
,
2
5
0
,
или же
$
5
2
5
,
0
0
0
(Основная сумма займа + проценты за первый год)
×
5
%
×
1
После третьего года выплата процентов
знак равно
$
2
7
,
5
6
2
.5
0
,
или же
$
5
5
1
,
2
5
0
Основная сумма займа + проценты за первый год
и два)
×
5
%
×
1
Общая сумма процентов к уплате через три года
знак равно
$
7
8
,
8
1
2
.
5
0
,
или же
$
2
5
,
0
0
0
+
$
2
6
,
2
5
0
+
$
2
7
,
5
6
2
.
5
0
\ begin {align} & \ text {После первого года, выплата процентов} = \ 25 000 долларов США \ text {,} \\ & \ text {или} \ 500 000 долларов США \ text {(Основная сумма займа)} \ times 5 \% \ times 1 \\ & \ text {После второго года выплата процентов} = \ 26 250 долларов США \ text {,} \\ & \ text {или} \ 525 000 долларов США \ text {(основная сумма кредита + проценты первого года)} \\ & \ times 5 \ % \ times 1 \\ & \ text {После третьего года, выплата процентов} = \ 27 562 доллара США.50 \ text {,} \\ & \ text {или} \ $ 551 250 \ text {Основная сумма займа + проценты за первый год} \\ & \ text {и два)} \ times 5 \% \ times 1 \\ & \ text {Общая сумма процентов к уплате через три года} = \ 78 812,50 долларов США \ text {,} \\ & \ text {или} \ 25 000 долларов США + \ 26 250 долларов США + \ 27 562,50 долларов США \\ \ end {выровнено}
После первого года проценты к уплате = 25000 долларов США или 500000 долларов США (основная сумма кредита) × 5% × 1 После второго года подлежащие выплате проценты = 26 250 долларов США или 525000 долларов США (основная сумма кредита + проценты первого года) × 5% × 1 После третьего года процентные выплаты = 27 562,50 долларов США или 551 250 долларов США по основной сумме кредита + проценты за первый и второй годы) × 5% × 1 Общая сумма процентов, подлежащих выплате через три года = 78 812 долларов США. 3 — \ 500 000 долл. США \\ \ end {выровнено}
3 — \ 500 000 долл. США \\ \ end {выровнено}
Общая сумма процентов, подлежащих уплате через три года = 78 812,50 долларов США или 500 000 долларов США (основная сумма кредита) × (1 + 0,05) 3 — 500 000 долларов США
Этот пример показывает, как формула для сложных процентов возникает из выплаты процентов по процентам, а также основной суммы.
Виды процентов — Сберегательные проценты
Различные типы интересов могут немного сбивать с толку. Мы собрали несколько определений, чтобы помочь вам понять некоторые различия.
Проценты
Если вы кладете деньги в банк, проценты — это деньги, которые вы зарабатываете, как процент от вашего депозита.Если вы должны деньги банку или компании-эмитенту кредитной карты, проценты — это процент от вашего баланса, который вы платите за использование денег банка или компании-эмитента кредитной карты. Обычно он отображается как годовая процентная ставка, например 6,00% годовых (pa = «годовых», что означает «каждый год»).
Простая процентная ставка или номинальная процентная ставка
Когда вы зарабатываете простые или номинальные проценты на банковском счете, они выплачиваются только из денег, которые вы внесли на свой счет, а не из доходов вашего счета (процентные платежи).Нет никаких преимуществ от увеличения вашего дохода,
Пример:
Когда вы зарабатываете 6,00% годовых на 10 000 долларов, имеющихся на вашем банковском счете, это означает, что вам выплачиваются проценты в размере 600 долларов в год.
Сложные проценты
Когда ваши деньги приносят сложные проценты на банковский счет, полученные проценты добавляются к вашему балансу на регулярной основе. Таким образом, не только ваши деньги приносят проценты, но и проценты приносят проценты. Он будет отображаться как годовая процентная ставка e.грамм. 6,00% годовых.
Пример:
Допустим, процентная ставка по счету составляет 6,00% годовых, и она выплачивается ежемесячно. Вы инвестируете 10 000 долларов 1 января и больше не собираетесь пополнять счет. В конце первого месяца вы получите проценты в размере 50,96 долларов за 31 день. Таким образом, за февраль будут начислены проценты на сумму 10 050,96 долларов США за 28 дней. К концу года ваш общий баланс составит 10 616,78 долларов США.
В конце первого месяца вы получите проценты в размере 50,96 долларов за 31 день. Таким образом, за февраль будут начислены проценты на сумму 10 050,96 долларов США за 28 дней. К концу года ваш общий баланс составит 10 616,78 долларов США.
Наш Savings Maximiser ежемесячно увеличивает проценты, что является большим преимуществом для ваших сбережений!
Эффективная годовая процентная ставка
Если у вас простая или номинальная процентная ставка на период менее одного года, вы можете рассчитать эффективную годовую процентную ставку, сложив заработанные проценты.
Пример:
Вы открываете Срочный депозит на 3 месяца на сумму 10 000 долларов США по ставке 6,70% годовых. Чтобы получить эффективную годовую ставку, вы предполагаете, что проценты будут начисляться каждые 3 месяца (т.е. добавить проценты к вашим первоначальным инвестициям и реинвестировать по той же ставке в течение еще 3 месяцев), в результате чего эффективная процентная ставка составит 6,87% годовых.
Формулы сложных процентов для единого платежа (другие периоды)
Процентная ставка и эквивалент
Формулы сложных процентов для единовременного платежа (другие периоды)
Перейти к вопросам, относящимся к теме ниже
Если процентный период и
период начисления сложных процентов не указывается, тогда под процентной ставкой понимается
годовой с годовой усложнением.Примеры:
«12% годовых»
означает, что процентная ставка составляет 12% годовых, начисляемых ежегодно.
«12% начисленная процентная ставка
ежемесячно »означает, что процентная ставка составляет 12% в год (не 12% в месяц),
начисляется ежемесячно. Таким образом, процентная ставка составляет 1% (12% / 12) в месяц.
«1% годовых в месяц
сложный ежемесячный «недвусмысленно.
Когда период начисления сложных процентов
не является ежегодным, проблемы должны решаться с точки зрения периода начисления сложных процентов, а не
годы.
Пример: если вложено 100 долларов
под 6% годовых, начисляемых ежемесячно, то будущая стоимость этих инвестиций
через 4 года составляет:
F = P (1 + i) n =
100 долларов (1 + 0.005) 48
= 100 (1.005) 48
= 100 долларов США (1,2705) = 127,05 долларов США
Обратите внимание, что процентная ставка
использованное выше: (6% / 12) = 0,5% в месяц = 0,005 в месяц, и что число
используемых периодов составляет 48 (месяцев), а не 4 (лет).
Процентная ставка и эквивалент
Формулы сложных процентов для единовременного платежа (другие периоды)
Вопрос 1
Вопрос 2
Вернуться к формулам сложных процентов для единовременного платежа (другие периоды)
Вернуться в меню «Учебные пособия по интересам и эквивалентности»
Вернуться в меню обучающих программ
Вопрос 1.
Используйте таблицы процентов. Предполагать
что $ 1000 инвестируется сроком на 4 года под 12% годовых.
ежеквартальный. Сколько будет на счету по истечении 4 лет?
Выберите ответ, щелкнув одну из букв ниже, или щелкните
«Просмотрите тему», если необходимо.
A F = 1000 долларов США (F / P, 12%, 4) = 1000 долларов США (1,574) = 1574 доллара США
B F = 1000 долларов (F / P, 12%, 16) = 1000 долларов (6,130) = 6 130 долларов
C F = 1000 долларов США (F / P, 3%, 4) = 1000 долларов США (1,126) = 1 126 долларов США
D F = 1000 долларов (F / P, 3%, 16) = 1000 долларов (1.605) = 1 605 долл. США
Обзор темы
Вопрос 2.
Используйте таблицы процентов. Сколько
теперь необходимо инвестировать под 6% годовых, начисляемых ежемесячно, чтобы накопить 1000 долларов.
через пять лет?
Выберите ответ, щелкнув одну из букв ниже, или щелкните
«Просмотрите тему», если необходимо.
A P = 1000 долларов (P / F, 6%, 60) = 1000 долларов (0,0303) = 30,30 долларов
B P = 1000 долларов (P / F, 0,5%, 60) = 1000 долларов (0,7414) = 741,37 долларов
C P = 1000 долларов (P / F, 0,5%, 5) = 1000 долларов (0. 9754) = 975,40 долл. США
9754) = 975,40 долл. США
D P = 1000 долларов (P / F, 6%, 5) = 1000 долларов (0,7473) = 747,30 долларов
Обзор темы
Использование простой формулы процента для расчета начисленных процентов
Результаты обучения
- Расчет простых процентов, полученных с учетом времени, ставки и основной суммы
- Рассчитайте основную сумму с учетом полученных процентов и установите ставку
- Рассчитать процентную ставку с учетом основной суммы и начисленных процентов
Вы знаете, что банки платят вам за то, чтобы они оставляли вам ваши деньги? Деньги, которые вы кладете в банк, называются основной суммой , [латекс] P [/ латекс], и банк выплачивает вам процентов , [латекс] I [/ латекс].Проценты рассчитываются как определенный процент от основной суммы долга; называется процентная ставка , [латекс] r [/ латекс]. Процентная ставка обычно выражается в процентах в год и рассчитывается с использованием десятичного эквивалента процента. Переменная времени [latex] t [/ latex] представляет количество лет, в течение которых деньги остаются на счете.
Простые проценты
Если сумма денег, [латекс] P [/ латекс], основная сумма, инвестируется на период [латекс] t [/ латекс] лет по годовой процентной ставке [латекс] r [/ латекс], сумма интерес, [латекс] я [/ латекс], заработано
[латекс] I = Prt [/ латекс]
, где
[латекс] \ begin {array} {ccc} \ hfill I & = & \ text {Interest} \ hfill \\ \ hfill P & = & \ text {Principal} \ hfill \\ \ hfill r & = & \ text {rate} \ hfill \\ \ hfill t & = & \ text {time} \ hfill \ end {array} [/ latex]
Процент, полученный по этой формуле, называется простым процентом.
Формула, которую мы используем для расчета простых процентов: [латекс] I = Prt [/ латекс]. Чтобы использовать формулу простого процента, мы подставляем значения для заданных переменных, а затем ищем неизвестную переменную. Может быть полезно систематизировать информацию, перечислив все четыре переменные и заполнив данную информацию.
Может быть полезно систематизировать информацию, перечислив все четыре переменные и заполнив данную информацию.
, пример
Найдите простой процент, полученный через [latex] 3 [/ latex] лет на [latex] \ text {\ $ 500} [/ latex] по процентной ставке [latex] \ text {6%.} [/ латекс]
Решение
Организуйте данную информацию в список.
[латекс] \ begin {array} {ccc} \ hfill I & = &? \ Hfill \\ \ hfill P & = & \ text {$ 500} \ hfill \\ \ hfill r & = & \ text {6%} \ hfill \ \ \ hfill t & = & \ text {3 года} \ hfill \ end {array} [/ latex]
Мы воспользуемся простой формулой процента, чтобы найти проценты.
| Напишите формулу. | [латекс] I = Prt [/ латекс] |
| Заменить данную информацию.Не забудьте указать процент в десятичной форме. | [латекс] I = \ влево (500 \ вправо) \ влево (0,06 \ вправо) \ влево (3 \ вправо) [/ латекс] |
| Упростить. | [латекс] I = 90 [/ латекс] |
| Проверьте свой ответ. Является ли [latex] \ text {\ $ 90} [/ latex] разумным процентом, заработанным на [latex] \ text {\ $ 500} [/ latex] за [latex] 3 [/ latex] года? | |
| За [latex] 3 [/ latex] года деньги заработали [latex] 18 \ text {%} [/ latex]. Если мы округлим до [латекс] 20 \ text {%} [/ latex], процентная ставка составила бы [латекс] 500 (0.20) [/ latex] или [latex] \ text {\ $ 100} [/ latex]. Да, [latex] \ text {\ $ 90} [/ latex] разумно. | |
| Напишите полное предложение, которое отвечает на вопрос. | Простой интерес — [латекс] \ text {\ $ 90} [/ латекс]. |
В следующем примере мы воспользуемся простой формулой процента, чтобы найти основную сумму.
, пример
Найдите инвестированный капитал, если проценты [latex] \ text {\ $ 178} [/ latex] были заработаны за [latex] 2 [/ latex] года по процентной ставке [latex] \ text {4%. } [/ латекс]
} [/ латекс]
Показать решение
Решение
Организуйте данную информацию в список.
[латекс] \ begin {array} {ccc} \ hfill I & = & \ text {$ 178} \ hfill \\ \ hfill P & = &? \ Hfill \\ \ hfill r & = & \ text {4%} \ hfill \ \ \ hfill t & = & \ text {2 года} \ hfill \ end {array} [/ latex]
Мы будем использовать формулу простого процента, чтобы найти основную сумму.
| Напишите формулу. | [латекс] I = Prt [/ латекс] |
| Заменить данную информацию. | [латекс] 178 = P \ влево (0,04 \ вправо) \ влево (2 \ вправо) [/ латекс] |
| Разделить. | [латекс] \ frac {178} {0,08} = \ frac {0,08P} {0,08} [/ латекс] |
| Упростить. | [латекс] 2,225 = П [/ латекс] |
| Проверьте свой ответ. Разве разумно, чтобы [latex] \ text {\ $ 2,225} [/ latex] заработал [latex] \ text {\ $ 178} [/ latex] за [latex] 2 [/ latex] года? | |
| [латекс] I = Prt [/ латекс] | |
| [латекс] 178 \ stackrel {?} {=} 2,225 \ left (0.04 \ вправо) \ влево (2 \ вправо) [/ латекс] | |
| [латекс] 178 = 178 \ квадратик \ галочка [/ латекс] | |
| Напишите полное предложение, которое отвечает на вопрос. | Основа — [латекс] \ text {\ $ 2,225} [/ латекс]. |
Теперь будем решать процентную ставку.
, пример
Найдите ставку, если принципал [latex] \ text {\ 8,200} [/ latex] заработал [latex] \ text {\ 3,772} [/ latex] процент в [latex] 4 [/ latex] годах.
Показать решение
Решение
Организуйте данную информацию.
[латекс] \ begin {array} {ccc} \ hfill I & = & \ text {\ $ 3,772} \ hfill \\ \ hfill P & = & \ text {\ 8200} \ hfill \\ \ hfill r & = &? \ Hfill \\ \ hfill t & = & \ text {4 года} \ hfill \ end {array} [/ latex]
Мы будем использовать простую формулу процента, чтобы найти ставку.
| Напишите формулу. | [латекс] I = Prt [/ латекс] |
| Заменить данную информацию. | [латекс] 3,772 = 8,200р \ влево (4 \ вправо) [/ латекс] |
| Умножить. | [латекс] 3,772 = 32,800р [/ латекс] |
| Разделить. | [латекс] \ frac {3,772} {32,800} = \ frac {32,800} {32,800} [/ латекс] |
| Упростить. | [латекс] 0,115 = r [/ латекс] |
| Запишите в процентах. | [латекс] \ text {11,5%} = r [/ латекс] |
| Проверьте свой ответ. Является ли [latex] 11,5 \ text {%} [/ latex] разумной ставкой, если [latex] \ text {\ $ 3,772} [/ latex] было заработано за [latex] 4 [/ latex] года? | |
| [латекс] I = Prt [/ латекс] | |
| [латекс] 3,772 \ stackrel {?} {=} 8,200 \ left (0.115 \ вправо) \ влево (4 \ вправо) [/ латекс] | |
| [латекс] 3,772 = 3,772 \ квадратик \ галочка [/ латекс] | |
| Напишите полное предложение, которое отвечает на вопрос. | Оценка была [латекс] 11,5 \ text {%} [/ latex]. |
Простые проценты | Финансы и рост
9.2 Простые проценты (EMA6M)
- Простые проценты
Простые проценты — это проценты, начисляемые только на первоначальную сумму, которую вы вложили.
В качестве простого примера простого интереса рассмотрим, сколько мы получим, вложив \ (\ text {R} \, \ text {1 000} \) на \ (\ text {1} \) год в банк. который платит \ (\ text {5} \% \) pa простой интерес.
На конец года у нас
\ begin {align *}
\ text {Интерес} & = \ text {R} \, \ text {1 000} \ times \ text {5} \% \\
& = \ text {R} \, \ text {1 000} \ times \ frac {5} {100} \\
& = \ text {R} \, \ text {1 000} \ times \ text {0,05} \\
& = \ текст {R} \, \ текст {50}
\ end {выровнять *}
При начальном сальдо \ (\ text {R} \, \ text {1 000} \) в начале года, итоговое сальдо в конце года, следовательно, будет
.
\ begin {align *}
\ text {Конечное сальдо} & = \ text {Начальное сальдо} + \ text {Проценты} \\
& = \ text {R} \, \ text {1 000} + \ text {R} \, \ text {50} \\
& = \ текст {R} \, \ текст {1 050}
\ end {выровнять *}
Начальное сальдо в финансовых расчетах часто называют основной суммой, обозначенной в данном примере как \ (P \) (\ (\ text {R} \, \ text {1 000} \)).Процентная ставка обычно обозначается как \ (i \) (\ (\ text {5} \% \) в этом примере, а «годовой год» означает год или год). Сумма процентов помечена \ (I \) (\ (\ text {R} \, \ text {50} \) в примере).
Итак, мы видим, что
\ [I = P \ times i \]
и
\ begin {align *}
\ text {Конечное сальдо} & = \ text {Начальное сальдо} + \ text {Проценты} \\
& = P + I \\
& = P + P \ times i \\ & = P \ left (1 + i \ right)
\ end {выровнять *}
Приведенные выше расчеты дают хорошее представление о том, как выглядит простая формула процента.Однако в примере показана инвестиция, срок действия которой составляет всего один год. Если инвестиция или ссуда рассчитаны на более длительный период, мы должны это учитывать. Мы используем символ \ (n \) для обозначения периода времени, который должен быть указан в годах.
Общая формула расчета простых процентов:
\ begin {align *}
A & = P \ влево (1 + в \ вправо) \\
\ text {Где:} & \\
A & = \ text {накопленная сумма (окончательная)} \\
P & = \ text {основная сумма (начальная)} \\
i & = \ text {проценты в десятичном формате} \\
n & = \ text {количество лет}
\ end {align *}
Рабочий пример 1: Расчет процентов по депозиту
Карин вкладывает \ (\ text {R} \, \ text {1 000} \) на специальный банковский счет, на который выплачивается простая процентная ставка \ (\ text {7} \% \) p.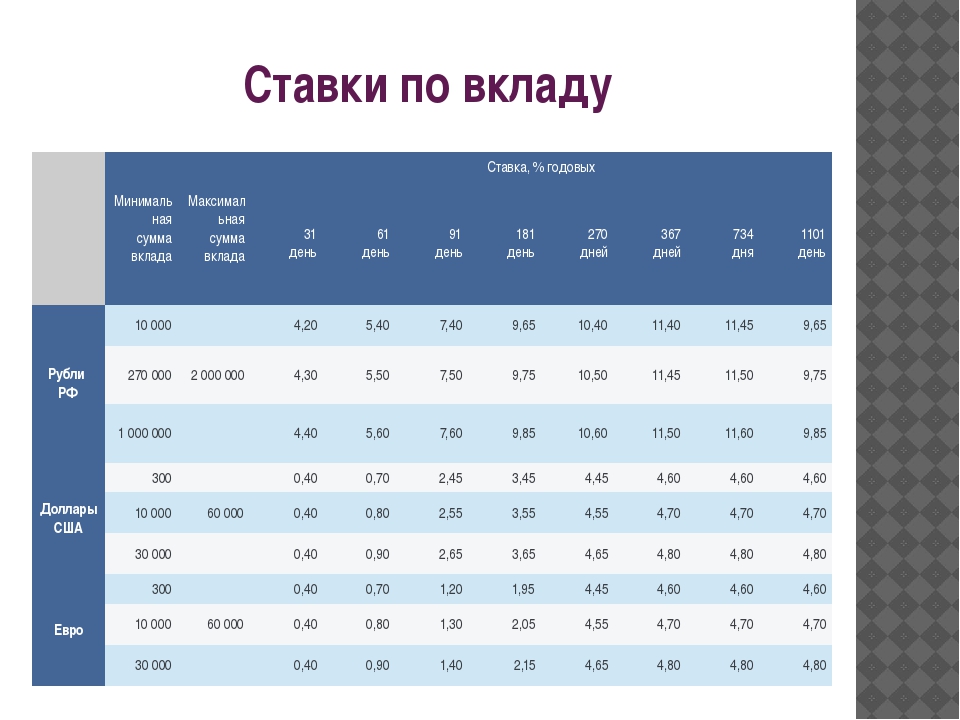 а. на \ (\ text {3} \) лет. Сколько будет на ее счету в конце срока инвестирования?
а. на \ (\ text {3} \) лет. Сколько будет на ее счету в конце срока инвестирования?
Запишите известные значения
\ begin {align *}
P & = \ text {1 000} \\
я & = \ текст {0,07} \\
n & = 3
\ end {align *}
Запишите формулу
\ [A = P \ left (1 + in \ right) \]
Заменить значения
\ begin {align *}
A & = \ text {1 000} \ left (1 + \ text {0,07} \ times 3 \ right) \\
& = \ текст {1 210}
\ end {align *}
Напишите окончательный ответ
По прошествии \ (\ text {3} \) лет у Карин будет \ (\ text {R} \, \ text {1 210} \) на своем банковском счете.
Рабочий пример 2: Расчет процентов по ссуде
Сара занимает \ (\ text {R} \, \ text {5 000} \) у своего соседа по согласованной простой процентной ставке \ (\ text {12,5} \% \) годовых. Она выплатит ссуду единовременно в конце \ (\ text {2} \) лет. Сколько ей придется заплатить соседу?
Запишите известные переменные
\ begin {align *}
P & = \ text {5 000} \\
я & = \ текст {0,125} \\
п & = 2
\ end {align *}
Запишите формулу
\ [A = P \ left (1 + in \ right) \]
Заменить значения
\ begin {align *}
A & = \ text {5 000} \ left (1 + \ text {0,125} \ times 2 \ right) \\
& = \ текст {6 250}
\ end {align *}
Напишите окончательный ответ
По прошествии \ (\ text {2} \) лет Сара заплатит своему соседу \ (\ text {R} \, \ text {6 250} \).
Мы можем использовать простую формулу процента, чтобы найти недостающие фрагменты информации. Например, если у нас есть сумма денег, которую мы хотим инвестировать в течение определенного количества времени для достижения целевой суммы, мы можем изменить порядок переменных, чтобы найти требуемую процентную ставку. Те же принципы применимы к определению периода времени, в течение которого нам нужно было бы инвестировать деньги, если бы мы знали основную сумму, накопленные суммы и процентную ставку.
Важно: Чтобы получить более точный ответ, попробуйте произвести все свои расчеты на калькуляторе за один раз.Это предотвратит влияние ошибок округления на ваш окончательный ответ.
Рабочий пример 3: Определение инвестиционного периода для достижения целевой суммы
Prashant вкладывает \ (\ text {R} \, \ text {30 000} \) на банковский счет с простой процентной ставкой \ (\ text {7,5} \% \) в год. Сколько лет должно он инвестирует для создания \ (\ text {R} \, \ text {45 000} \)?
Запишите известные переменные
\ begin {align *}
A & = \ text {45 000} \\
P & = \ text {30 000} \\
я & = \ текст {0,075}
\ end {align *}
Запишите формулу
\ [A = P \ left (1 + in \ right) \]
Подставьте значения и решите для \ (n \)
\ begin {align *}
\ text {45 000} & = \ text {30 000} \ left (1 + \ text {0,075} \ times n \ right) \\
\ frac {\ text {45 000}} {\ text {30 000}} & = 1 + \ text {0,075} \ times n \\
\ frac {\ text {45 000}} {\ text {30 000}} — 1 & = \ text {0,075} \ times n \\
\ frac {\ left (\ frac {\ text {45 000}} {\ text {30 000}} \ right) -1} {\ text {0,075}} & = n \\
n & = 6 \ frac {2} {3}
\ end {align *}
Напишите окончательный ответ
Чтобы \ (\ text {R} \, \ text {45 000} \) из \ (\ text { R} \, \ text {30 000} \) по простой процентной ставке \ (\ text {7,5} \% \) p.а.
Рабочий пример 4: Расчет простой процентной ставки для достижения желаемого роста
По какой простой процентной ставке следует инвестировать Фрите, если она хочет вырасти \ (\ text {R} \, \ text {2 500} \) до \ (\ text {R} \, \ text {4 000} \) в \ (\ text {5} \) лет?
Запишите известные переменные
\ begin {align *}
A & = \ text {4 000} \\
P & = \ text {2 500} \\
n & = 5
\ end {align *}
Запишите формулу
\ [A = P \ left (1 + in \ right) \]
Подставьте значения и решите для \ (i \)
\ begin {align *}
\ text {4 000} & = \ text {2 500} \ left (1 + i \ times 5 \ right) \\
\ frac {\ text {4 000}} {\ text {2 500}} & = 1 + i \ times 5 \\
\ frac {\ text {4 000}} {\ text {2 500}} — 1 & = i \ times 5 \\
\ frac {\ left (\ frac {\ text {4 000}} {\ text {2 500}} \ right) — 1} {5} & = i \\
я & = \ текст {0,12}
\ end {align *}
Напишите окончательный ответ
Простая процентная ставка \ (\ text {12} \% \) p.а. потребуется при инвестировании \ (\ text {R} \, \ text {2 500} \) на \ (\ text {5} \) лет, чтобы стать \ (\ text {R} \, \ text {4 000} \).
Siyavula Practice дает вам доступ к неограниченному количеству вопросов с ответами, которые помогут вам в обучении. Тренируйтесь где угодно, когда угодно и на любом устройстве!
Зарегистрируйтесь, чтобы попрактиковаться сейчас
Упражнение 9.1
Сумма \ (\ text {R} \, \ text {3 500} \) инвестируется на сберегательный счет, на который выплачиваются простые проценты по ставке \ (\ text {7,5} \% \) в год. .Рассчитайте остаток, накопленный к концу \ (\ text {2} \) лет.
\ begin {align *}
P & = \ text {3 500} \\
я & = \ текст {0,075} \\
п & = 2 \\
A & =? \\\\
А & = Р (1 + дюйм) \\
A & = \ text {3 500} (1 + (\ text {0,075}) (2)) \\
A & = \ text {3 500} (\ text {1,15}) \\
A & = \ text {R} \, \ text {4 025}
\ end {выровнять *}
Сумма \ (\ text {R} \, \ text {4 090} \) инвестируется на сберегательный счет, на который выплачиваются простые проценты по ставке \ (\ text {8} \% \) в год.Рассчитайте остаток, накопленный к концу \ (\ text {4} \) лет.
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & =? \\
P & = \ text {4 090} \\
п & = 4 \\
i & = \ frac {8} {100} = \ text {0,08}
\ end {align *}
\ begin {align *}
А & = Р (1 + дюйм) \\
& = \ text {R} \, \ text {4 090} \ left (\ text {1} + \ left (\ text {0,08} \ right) \ times \ text {4} \ right) \\
& = \ text {R} \, \ text {5 398,80}
\ end {align *}
Сумма \ (\ text {R} \, \ text {1 250} \) инвестируется в сберегательный счет, на который выплачиваются простые проценты по ставке \ (\ text {6} \% \) в год.Рассчитайте остаток, накопленный к концу \ (\ text {6} \) лет.
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & =? \\
P & = \ text {1 250} \\
п & = 6 \\
i & = \ frac {6} {100} = \ text {0,06}
\ end {align *}
Простая формула процента:
\ begin {align *}
А & = Р (1 + дюйм) \\
& = \ text {R} \, \ text {1 250} \ left (\ text {1} + \ left (\ text {0,06} \ right) \ times \ text {6} \ right) \\
& = \ text {R} \, \ text {1 700,00}
\ end {align *}
Сумма \ (\ text {R} \, \ text {5 670} \) инвестируется на сберегательный счет, на который выплачиваются простые проценты по ставке \ (\ text {8} \% \) в год.Рассчитайте остаток, накопленный к концу \ (\ text {3} \) лет.
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & =? \\
P & = \ text {5 670} \\
п & = 3 \\
i & = \ frac {8} {100} = \ text {0,08}
\ end {align *}
Простая формула процента:
\ begin {align *}
А & = Р (1 + дюйм) \\
& = \ text {R} \, \ text {5 670,00} \ left (\ text {1} + \ left (\ text {0,08} \ right) \ times \ text {3} \ right) \ \
& = \ text {R} \, \ text {7 030,80}
\ end {align *}
Кредит в размере \ (\ text {R} \, \ text {300} \) со ставкой \ (\ text {8} \% \) на \ (\ text {1} \) год.
\ begin {align *}
P & = 300 \\
я & = \ текст {0,08} \\
п & = 1 \\
A & =? \\ \\
А & = Р (1 + дюйм) \\
A & = 300 (1+ (\ text {0,08}) (1)) \\
A & = 300 (\ text {1,08}) \\
A & = \ текст {R} \, \ text {324}
\ end {выровнять *}
Вложение \ (\ text {R} \, \ text {2 250} \) по ставке \ (\ text {12,5} \% \) p.а. на \ (\ text {6} \) лет.
\ begin {align *}
P & = \ text {2 250} \\
я & = \ текст {0,125} \\
п & = 6 \\
A & =? \\ \\
А & = Р (1 + дюйм) \\
A & = \ text {2 250} (1+ (\ text {0,125}) (6)) \\
A & = \ text {2 250} (\ text {1,75}) \\
A & = \ text {R} \, \ text {3 937,50}
\ end {выровнять *}
Банк предлагает сберегательный счет, на который выплачиваются простые проценты по ставке \ (\ text {6} \% \) в год.Если вы хотите накопить \ (\ text {R} \, \ text {15 000} \) за \ (\ text {5} \) лет, сколько вам следует инвестировать сейчас?
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & = \ text {R} \, \ text {15 000} \\
P & =? \\
i & = \ frac {6} {100} = \ text {0,06} \\
n & = 5
\ end {align *}
Простая формула процента:
\ begin {align *}
А & = Р (1 + дюйм) \\
\ text {R} \, \ text {15 000} & = P \ left (\ text {1} + \ left (\ text {0,06} \ right) \ times \ text {5} \ right) \\
P & = \ frac {\ text {R} \, \ text {15 000}} {\ text {1,3}} \\
& = \ text {R} \, \ text {11 538,46}
\ end {align *}
Салли хотела подсчитать, сколько лет ей нужно инвестировать в \ (\ text {R} \, \ text {1 000} \), чтобы накопить \ (\ text {R} \, \ text {2 500} \).Ей предложили простую процентную ставку в размере \ (\ text {8,2} \% \) годовых. Через сколько лет деньги вырастут до \ (\ text {R} \, \ text {2 500} \)?
\ begin {align *}
A & = \ text {2 500} \\
P & = \ text {1 000} \\
я & = \ текст {0,082} \\
п & =? \\ \\
А & = Р (1 + дюйм) \\
\ text {2 500} & = \ text {1 000} (1+ (\ text {0,082}) (n)) \\
\ frac {\ text {2 500}} {\ text {1 000}} & = 1 + \ text {0,082} n \\
\ frac {\ text {2 500}} {\ text {1 000}} — 1 & = \ text {0,082} n \\
\ left (\ frac {\ text {2 500}} {\ text {1 000}} — 1 \ right) \ div \ text {0,082} & = n \\
п & = \ текст {18,3}
\ end {выровнять *}
Потребуется \ (\ text {19} \) лет, чтобы \ (\ text {R} \, \ text {1 000} \) превратился в \ (\ text {R} \, \ text {2 500} \ ) в \ (\ text {8,2} \% \) p.а.
Джозеф положил \ (\ text {R} \, \ text {5 000} \) на сберегательный счет на пятый день рождения сына. Когда его сыну исполнилось \ (\ text {21} \), остаток на счете вырос до \ (\ text {R} \, \ text {18 000} \). Если использовались простые проценты, рассчитайте ставку, по которой были инвестированы деньги.
\ begin {align *}
A & = \ text {18 000} \\
P & = \ text {5 000} \\
я & =? \\
п & = 21-5 = 16 \\ \\
А & = Р (1 + дюйм) \\
\ text {18 000} = \ text {5 000} (1+ (i) (16)) \\
\ frac {\ text {18 000}} {\ text {5 000}} & = 1 + 16i \\
\ frac {\ text {18 000}} {\ text {5 000}} — 1 & = 16i \\
\ left (\ frac {\ text {18 000}} {\ text {5 000}} — 1 \ right) \ div 16 & = i \\
я & = \ текст {0,1625}
\ end {выровнять *}
Процентная ставка, по которой были вложены деньги, составляла \ (\ text {16,25} \% \).
Когда его сын был \ (\ text {6} \)
лет, Метули внес депозит в размере
\ (\ text {R} \, \ text {6 610} \)
в банке. Инвестиции выросли по простой процентной ставке и
когда сын Метули был
\ (\ text {18} \) лет, значение
инвестиции было
\ (\ text {R} \, \ text {11 131,24} \).
По какой ставке были вложены деньги? Дайте правильный ответ с точностью до одного десятичного знака.
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & = \ text {R} \, \ text {11 131,24} \\
P & = \ text {R} \, \ text {6 610} \\
я & =? \\
n & = 18 — 6 = 12
\ end {align *}
В вопросе говорится, что инвестиции «выросли по простой процентной ставке», поэтому мы должны использовать простую формулу процента.Чтобы рассчитать процентную ставку, нам нужно сделать \ (i \)
предмет формулы:
\ begin {align *}
А & = Р (1 + дюйм) \\
\ frac {A} {P} & = 1 + в \\
\ frac {A} {P} -1 & = в \\
\ frac {\ frac {A} {P} -1} {n} & = i \\
\ text {Следовательно} i & = \ frac {\ left (\ frac {\ text {} \, \ text {11 131,24}} {\ text {6 610}} \ right) — 1} {\ text { 12}} \\
& = \ текст {0,057} \\
& = \ text {5,7} \% \ text {в год}
\ end {align *}
Когда его сын был \ (\ text {6} \)
лет, Филипп внес депозит в размере
\ (\ text {R} \, \ text {5 040} \)
в банке.Инвестиции выросли по простой процентной ставке и
когда сын Филиппа был
\ (\ text {18} \) лет, значение
инвестиции было
\ (\ text {R} \, \ text {7 338,24} \).
По какой ставке были вложены деньги? Ответьте правильно с точностью до одного десятичного знака.
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & = \ text {R} \, \ text {7 338,24} \\
P & = \ text {R} \, \ text {5 040} \\
я & =? \\
n & = 18 — 6 = 12
\ end {align *}
В вопросе говорится, что инвестиции «выросли по простой процентной ставке», поэтому мы должны использовать простую формулу процента.Чтобы рассчитать процентную ставку, нам нужно сделать \ (i \)
предмет формулы:
\ begin {align *}
А & = Р (1 + дюйм) \\
\ frac {A} {P} & = 1 + в \\
\ frac {A} {P} -1 & = в \\
\ frac {\ frac {A} {P} -1} {n} & = i \\
\ text {Следовательно} i & = \ frac {\ left (\ frac {\ text {} \, \ text {7 338,24}} {\ text {5 040}} \ right) — 1} {\ text { 12}} \\
& = \ текст {0,038} \\
& = \ text {3,8} \% \ text {в год}
\ end {align *}
Когда его сын был \ (\ text {10} \)
лет, Лефу внес депозит в размере
\ (\ text {R} \, \ text {2 580} \)
в банке.Инвестиции выросли по простой процентной ставке и
когда сын Лефу был
\ (\ text {20} \) лет, значение
инвестиции было
\ (\ text {R} \, \ text {3 689,40} \).
По какой ставке были вложены деньги? Ответьте правильно с точностью до одного десятичного знака.
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & = \ text {R} \, \ text {3 689,40} \\
P & = \ text {R} \, \ text {2 580} \\
я & =? \\
n & = 20 — 10 = 10
\ end {align *}
В вопросе говорится, что инвестиции «выросли по простой процентной ставке», поэтому мы должны использовать простую формулу процента.Чтобы рассчитать процентную ставку, нам нужно сделать \ (i \)
предмет формулы:
\ begin {align *}
А & = Р (1 + дюйм) \\
\ frac {A} {P} & = 1 + в \\
\ frac {A} {P} -1 & = в \\
\ frac {\ frac {A} {P} -1} {n} & = i \\
\ text {Следовательно} i & = \ frac {\ left (\ frac {\ text {} \, \ text {3 689,40}} {\ text {2 580}} \ right) — 1} {\ text { 10}} \\
& = \ текст {0,043} \\
& = \ text {4,3} \% \ text {в год}
\ end {align *}
Абдул хочет инвестировать \ (\ text {R} \, \ text {1 080} \) по простой процентной ставке \ (\ text {10,9} \% \) p.а.
Через сколько лет деньги вырастут до \ (\ text {R} \, \ text {3 348} \)? Округлите до , чтобы получить ответ до ближайшего года.
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & = \ text {R} \, \ text {3 348} \\
P & = \ text {R} \, \ text {1 080} \\
i & = \ frac {\ text {10,9}} {100} = \ text {0,109} \\
п & =?
\ end {align *}
Чтобы вычислить количество лет, нам нужно сделать \ (n \) предметом формулы:
\ begin {align *}
А & = Р (1 + дюйм) \\
\ frac {A} {P} & = 1 + в \\
\ frac {A} {P} -1 & = в \\
\ frac {\ frac {A} {P} -1} {i} & = n \\
\ text {Следовательно} n & = \ frac {\ left (\ frac {\ text {3 348}} {\ text {1 080}} \ right) — \ text {1}} {\ text {0,109}} \ \
& = \ текст {19,3} \\
& = \ text {20} \ text {years} \ quad \ Leftarrow \ text {округлить до ближайшего целого числа}
\ end {align *}
Эндрю хочет инвестировать \ (\ text {R} \, \ text {3 010} \) по простой процентной ставке \ (\ text {11,9} \% \) p.а.
Через сколько лет деньги вырастут до \ (\ text {R} \, \ text {14 448} \)? Округлите до , чтобы получить ответ до ближайшего года.
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & = \ text {R} \, \ text {14 448} \\
P & = \ text {R} \, \ text {3 010} \\
i & = \ frac {\ text {11,9}} {100} = \ text {0,119} \\
п & =?
\ end {align *}
Чтобы вычислить количество лет, нам нужно сделать \ (n \) предметом формулы:
\ begin {align *}
А & = Р (1 + дюйм) \\
\ frac {A} {P} & = 1 + в \\
\ frac {A} {P} -1 & = в \\
\ frac {\ frac {A} {P} -1} {i} & = n \\
\ text {Следовательно} n & = \ frac {\ left (\ frac {\ text {14 448}} {\ text {3 010}} \ right) — \ text {1}} {\ text {0,119}} \ \
& = \ текст {31,9} \\
& = \ text {32} \ text {years} \ quad \ Leftarrow \ text {округлить до ближайшего целого числа}
\ end {выровнять *}
Округляя до ближайшего года, потребуется \ (\ text {32} \) лет, чтобы достичь цели по экономии \ (\ text {R} \, \ text {14 448} \).
.
