Реквизиты и контакты

Реквизиты ПАО «НБД-Банк»:

• Кор. счет: 30101810400000000705
• БИК: 042202705
• ИНН: 5200000222
• КПП: 526001001
• Код ОКВЭД: 64.19
• Код ОКПО: 10668259
• E-mail: [email protected]

Главная бухгалтерия:

Котова Ирина Владимировна — главный бухгалтер
Башева Елена Николаевна — заместитель главного бухгалтера
Карабасова Ирина Валерьевна — заместитель главного бухгалтера

О подтверждении банковских гарантий:

Главная бухгалтерия.

Лицо, ответственное за подтверждение предоставленных банковских гарантий — Гараничева Ирина Владимировна
Контактный телефон: (831) 22-000-22 (доб. 3349)
E-mail: [email protected]

Реквизиты для международных переводов:

NBD-Bank
SWIFT: NBDBRU2N
6, Gorky Sqr., Nizhny Novgorod, 603950, Russia
Tel.: +7 831 22 000 22;
Fax: +7 831 434 39 48

Сведения о Банке:

Полное наименование:

Публичное акционерное общество «НБД-Банк»;
NBD-Bank, Public Joint-Stock Company

Сокращенное наименование:

ПАО «НБД-Банк»;
NBD-Bank

Координаты ПАО «НБД-Банк»:

Местонахождение органов управления:
603950, Россия, г. Нижний Новгород, пл. Горького, 6

Телефон: (831) 22-000-22 (многоканальный)

Факс: (831) 434-39-48

Регистрационный номер:

1966

Дата регистрации Банком России:

27.07.1992

Основной государственный регистрационный номер (МНС России):

1025200000022

Дата внесения записи в Единый государственный реестр юридических лиц:

07.08.2002

Генеральная лицензия ЦБ РФ №1966 от 12.08.2015, Без ограничения срока действия

Генеральная лицензия ЦБ РФ №1966 c QR-кодом от 12.08.2015, Без ограничения срока действия

Регистрирующий орган:
Центральный банк Российской Федерации

ПАО «НБД-Банк» включен в реестр банков — участников системы обязательного страхования вкладов 16 декабря 2004 года под номером 299

Прочие лицензии, на основании которых действует Банк:

Аудиторская организация:

По стандартам Российской Федерации:

Общество с ограниченной ответственностью «Риан-Аудит»

• место нахождения: 127642, Россия, г. Москва, проезд Дежнёва, д.1, эт.10, пом. XII, оф. 1005
• основной государственный регистрационный номер: 1037709050664
• ИНН: 7709426578;
• членство в саморегулируемой организации аудиторов: член Саморегулируемой организации аудиторов Ассоциации «Содружество». Основной регистрационный номер записи о внесении сведений в Реестр СРО: 12006049162. Дата внесения записи в реестр: 18.02.2020. Место нахождения: 119192, Россия, г.Москва, проспект Мичуринский, д.21, корп. 4
• Дата завершения проверки за 2020 год и выдача аудиторского заключения ООО «Риан-Аудит» 24.03.2021. Вид отчетности, в отношении которой проводилась проверка: годовая бухгалтерская (финансовая) отчетность.

По международным стандартам:

Акционерное общество «Бейкер Тилли Рус»

• место нахождения: 125284, г. Москва, Хорошёвское шоссе, д.32А, пом./каб. VII/57
• основной государственный регистрационный номер: 1027700115409;
• ИНН: 7704154440;
• членство в саморегулируемой организации аудиторов: член Саморегулируемой организации аудиторов Ассоциации «Содружество». Основной регистрационный номер записи о внесении сведений в Реестр СРО: 12006010438. Дата внесения записи в реестр: 17.01.2020. Место нахождения: 119192, Россия, г.Москва, проспект Мичуринский, д.21, корп. 4
• Дата завершения проверки за 2020 год и выдача аудиторского заключения АО «Бейкер Тилли Рус» 19.04.2021. Вид отчетности, в отношении которой проводилась проверка: годовая финансовая отчетность.

Банковский надзор за деятельностью кредитной организации ПАО «НБД-Банк» (рег.№1966) осуществляет Служба текущего банковского надзора Банка России.

Телефоны Контактного центра Центрального банка Российской Федерации: 8-800-250-40-72, 8-495-771-91-00.

Надзор за соблюдением требований законодательства Российской Федерации в сфере защиты прав потребителей финансовых услуг осуществляет Служба по защите прав потребителей и обеспечению доступности финансовых услуг Банка России. Обращение о нарушении действиями (бездействием) кредитной организации законодательства Российской Федерации, а также охраняемых законом прав и интересов физических и юридических лиц, может быть направлено для рассмотрения в Банк России через интернет-приемную.

Для урегулирования досудебных споров потребитель должен обратиться к финансовому уполномоченному. Обращение может быть направлено в электронной форме на официальном сайте www.finombudsman.ru или в письменной форме. Прием и рассмотрение обращений осуществляется финансовым уполномоченным бесплатно.

Номер телефона службы обеспечения деятельности финансового уполномоченного: 8 (800) 200-00-10 (бесплатный звонок по России).

Почтовый адрес службы обеспечения деятельности финансового уполномоченного: 119017, г. Москва, Старомонетный переулок, дом 3, получатель АНО «СОДФУ».

Лицо, ответственное за содержание сайта – Корень Олег Иванович
Контактный телефон: (831) 22-000-22 (доб. 3139).
E-mail: [email protected]

Реквизиты Фонда ИЖС

ГУП «ФОНД ПОДДЕРЖКИ ИЖС»

Адрес: 308600, РФ, г. Белгород, ул. Князя Трубецкого, д. 28

Тел: (4722) 27-37-90

Факс: (4722) 30-84-79

Web: https://www. beligs.ru/

E-mail: Этот адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

ИНН 312 301 7088

КПП 312 301 001

ОКОНХ 96190

ОКПО 2222 4734

ОГРН 102 310 165 3740 

Генеральный директор: Антон Александрович Иванов, действующий на основании устава
Начальник финансово-экономического управления / Главный бухгалтер: Капаций Татьяна Анатольевна

Реквизиты для оплаты в ПАО Банк ВТБ

Получатель: ГУП «ФОНД ПОДДЕРЖКИ ИЖС»

ИНН 3123017088 / КПП 312301001

Филиал «Центральный» Банка ВТБ (ПАО) в г. Москве

ИНН 7702070139 / КПП 770943002

Расчетный счет № 40602810210160000001

БИК 044525411

Корреспондентский счет 30101810145250000411

Реквизиты для оплаты в ПАО Банк «Открытие»

Получатель: ГУП «ФОНД ПОДДЕРЖКИ ИЖС»

ИНН 3123017088 / КПП 312301001

БАНК ФИЛИАЛ ЦЕНТРАЛЬНЫЙ ПАО БАНКА «ФК ОТКРЫТИЕ»

ИНН 7702070139 / КПП 770943002

Расчетный счет № 40601810202070000001

БИК 044525297

Корреспондентский счет 30101810945250000297

Реквизиты для оплаты в АО УКБ «БелгородСоцбанк»

Получатель: ГУП «ФОНД ПОДДЕРЖКИ ИЖС»

ИНН 3123017088 / КПП 312301001

АО УКБ «БелгородСоцбанк»

ИНН 7702070139 / КПП 770943002

Расчетный счет № 40602810500010000052

БИК 041403701

Корреспондентский счет 30101810100000000701

Реквизиты БМВ Банк.

В настоящем Разделе представлена информация о реквизитах Банка.

Внимание! При погашении кредита данные реквизиты не используются. Реквизиты для погашения кредита безналичным путем Вы можете найти в Разделе Способы погашения кредита.

Полное наименование Банка:	Общество с ограниченной ответственностью «БМВ Банк»
Сокращенное наименование Банка:	«БМВ Банк» ООО
Сокращенное наименование Банка на английском и немецком языках:	«BMW Bank» OOO
Юридический адрес:	125212, Москва, Ленинградское шоссе, д. 39А, стр. 1 125212, Moscow, Leningradskoe Shosse 39A, building 1
Фактический адрес:	125212, Москва, Ленинградское шоссе, д. 39А, стр. 1 125212, Moscow, Leningradskoe Shosse 39A, building 1
Для рублевых операций/ rub:	корр. счет/corr. account 30101810145250000770 в ГУ Банка России по ЦФО БИК 044525770
Для операций в долларах США:	корр. счет № 30109840887000000001 в Московский филиал ПАО РОСБАНК Г. Москвы, SWIFT RSBNRUMMXXX (Банк-корреспондент для расчетов The Bank of New York Mellon, SWIFT IRVT US3N)
Для операций в ЕВРО:	корр. счет № 30109978487000000001  в Московский филиал ПАО РОСБАНК Г. Москвы, SWIFT RSBNRUMMXXX (Банк-корреспондент для расчетов Societe Generale S.A., Paris, SWIFT SOGE FR PP)

ОГРН/ OGRN 1085000001998, дата внесения 17. 03.2008 ИНН/ INN 5047093433 КПП/KPP 997950001 ОКПО/OKPO 84405943 ОКОГУ/OKOGU 1500010 ОКАТО/OKATO 45277565000 ОКТМО/OKTMO 45336000 ОКФС /OKFS 23 ОКОПФ/OKOPF 12300 ОКВЭД/OKVED 64.19

Председатель Правления Морозова Анна Борисовна, действующая на основании Устава Chairman of the Executive Board Morozova A.B., acting on the basis of the Charter

Главный бухгалтер Градюшко Екатерина Александровна Chief Accountant Gradushko Ekaterina

Реквизиты НГУ

Полное наименование	Федеральное государственное автономное образовательное учреждение высшего образования «Новосибирский национальный исследовательский государственный университет»
Сокращенное наименование	Новосибирский государственный университет, НГУ
Англоязычная транскрипция (полное наименование)	Novosibirsk State University
Англоязычная транскрипция (сокращенное наименование)	NSU
Руководитель НГУ	Ректор Михаил Петрович Федорук, действующий на основании Устава НГУ
Главный бухгалтер	Тарских Надежда Алексеевна, тел. +7 (383) 363-40-04
Юридический (фактический) адрес	630090, Новосибирская область, г. Новосибирск, ул. Пирогова, 2
ИНН	5408106490
КПП	540801001
Реквизиты в казначействе для всех перечислений в рублях, кроме валютных платежей и рублевых платежей для нерезидентов	Получатель: УФК по Новосибирской области (НГУ л/с 30516Щ44680) Банк получателя: СИБИРСКОЕ ГУ БАНКА РОССИИ//УФК по Новосибирской области г. Новосибирск Казначейский счет № 03214643000000015100 ЕКС (кор/сч) № 40102810445370000043 БИК ТОФК 015004950 КБК 00000000000000000130 (доходы от оказания услуг, выполнение НИР, госконтракты) ОКПО 02068930 ОКТМО 50701000 ОГРН 1025403658565
Для перечислений в НГУ в Евро	BENEFICIARY: Acc. N 40503978716034200058 Novosibirsk State University INN 5408106490 Address: Russia, 630090, Novosibirsk, Pirogova Street, 2 ACCOUNT HOLDING INSTITUTION: VTB BANK (PJSC) TSENTRALNYI BRANCH, MOSCOW SWIFT: VTBRRUM2MS2 Cor.acc №30101810145250000411 with PJSC VTB BANK, Moscow, SWIFT – VTBRRUMM
Для перечислений в НГУ в долларах США	BENEFICIARY: Acc. N 40503840416034200091 Novosibirsk State University INN 5408106490 Address: Russia, 630090, Novosibirsk, Pirogova Street, 2 ACCOUNT HOLDING INSTITUTION: VTB BANK (PJSC) TSENTRALNYI BRANCH, MOSCOW SWIFT: VTBRRUM2MS2 Cor.acc №30101810145250000411 with PJSC VTB BANK, Moscow, SWIFT – VTBRRUMM
Для перечислений в НГУ в рублях (для иностранных граждан и иностранных организаций)*	Банк получателя – Филиал «Центральный» Банка ВТБ (ПАО) в г. Москве БИК банка 044525411 Кор. счет 30101810145250000411 Р/с получателя 40503810716034000002 Наименование получателя — Новосибирский государственный университет Адрес — 630090, г. Новосибирск, ул. Пирогова, 2 ИНН 5408106490, КПП 540801001
*в назначении платежа обязательно указать	1. Код вида валютной операции в фигурных скобках { }: 20100 — Расчеты нерезидента в виде предварительной оплаты (аванс) 20200 — Расчеты нерезидента за выполненные резидентом работы, оказанные услуги (оплата, доплата после выполнения работ, оказания услуг) 2. Дату и номер договора 3. Назначение платежа (например, за обучение Иванова И.И.)

Контакты | inter-systems.ru

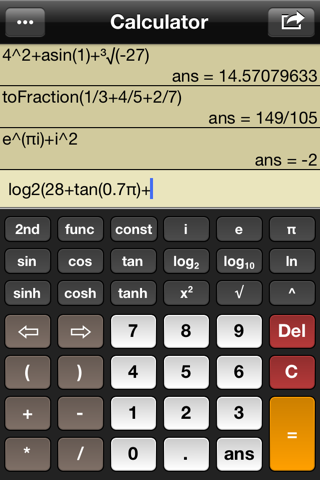
Вероятностный выбор модели с AIC, BIC и

леев

Последнее обновление 28 августа 2020 г.

Выбор модели — это проблема выбора одной из множества моделей-кандидатов.

Обычно выбирают модель, которая лучше всего работает с набором тестовых данных удержания, или оценивают производительность модели, используя метод повторной выборки, такой как k-кратная перекрестная проверка.

Альтернативный подход к выбору модели включает использование вероятностных статистических показателей, которые пытаются количественно оценить как производительность модели на обучающем наборе данных, так и сложность модели.Примеры включают критерий Акаике и байесовский информационный критерий и минимальную длину описания.

Преимущество этой статистики информационных критериев состоит в том, что они не требуют набора тестов выдержки, хотя ограничение состоит в том, что они не принимают во внимание неопределенность моделей и могут привести к выбору слишком простых моделей.

В этом посте вы найдете вероятностную статистику для выбора модели машинного обучения.

Прочитав этот пост, вы будете знать:

• Выбор модели — это проблема выбора одной из множества моделей-кандидатов.
• Akaike и байесовский информационный критерий — это два способа оценки модели на основе ее логарифмической вероятности и сложности.
• Minimum Description Length предоставляет еще один метод оценки из теории информации, который может быть эквивалентен BIC.

Начните свой проект с моей новой книги «Вероятность машинного обучения», включающей пошаговых руководств и файлы исходного кода Python для всех примеров.

Приступим.

Вероятностные критерии выбора модели AIC, BIC и MDL
Фото Гильхема Веллута, некоторые права защищены.

Обзор

Это руководство разделено на пять частей; их:

1. Проблема выбора модели
2. Выбор вероятностной модели
3. Информационный критерий Акаике
4. Байесовский информационный критерий
5. Минимальная длина описания

Проблема выбора модели

Выбор модели — это процесс подгонки нескольких моделей к данному набору данных и выбора одной из всех остальных.

Выбор модели: оценка производительности различных моделей с целью выбора лучшей.

— стр. 222, Элементы статистического обучения, 2016 г.

Это может применяться при обучении без учителя, например выбор модели кластеризации или контролируемого обучения, например выбор прогнозной модели для задачи регрессии или классификации. Это также может быть подзадача моделирования, например, выбор функций для данной модели.

Есть много общих подходов, которые можно использовать для выбора модели.Например, в случае обучения с учителем три наиболее распространенных подхода:

• Наборы данных для обучения, проверки и тестирования.
• Методы передискретизации.
• Вероятностная статистика.

Самый простой и надежный метод выбора модели включает подгонку моделей-кандидатов к обучающему набору, настройку их на проверочный набор данных и выбор модели, которая лучше всего работает с тестовым набором данных в соответствии с выбранной метрикой, например точностью или ошибкой.Проблема с этим подходом в том, что он требует большого количества данных.

Методы повторной выборки пытаются достичь того же, что и подход обучения / проверки / тестирования к выбору модели, хотя и с использованием небольшого набора данных. Примером является k-кратная перекрестная проверка, где обучающий набор разбивается на множество пар поезд / тест, и модель подбирается и оценивается для каждой. Это повторяется для каждой модели, и выбирается модель с наилучшим средним баллом по k-кратной шкале. Проблема с этим и предыдущим подходом заключается в том, что оценивается только производительность модели, независимо от сложности модели.

Третий подход к выбору модели пытается объединить сложность модели с производительностью модели в оценку, а затем выбрать модель, которая минимизирует или максимизирует оценку.

Мы можем назвать этот подход выборкой статистической или вероятностной модели, поскольку в методе оценки используется вероятностная структура.

Хотите узнать вероятность для машинного обучения

Пройдите мой бесплатный 7-дневный ускоренный курс электронной почты (с образцом кода).

Нажмите, чтобы зарегистрироваться, а также получите бесплатную электронную версию курса в формате PDF.

Загрузите БЕСПЛАТНЫЙ мини-курс

Выбор вероятностной модели

Вероятностный выбор модели (или «информационные критерии») обеспечивает аналитический метод оценки и выбора среди моделей-кандидатов.

Модели

оцениваются как по их производительности в обучающем наборе данных, так и по сложности модели.

• Модель Производительность .Насколько хорошо модель-кандидат работает с обучающим набором данных.
• Сложность модели . Насколько сложна модель обученного кандидата после обучения.

Характеристики модели могут быть оценены с использованием вероятностной структуры, такой как логарифмическая вероятность в рамках оценки максимального правдоподобия. Сложность модели можно оценить как количество степеней свободы или параметров в модели.

Исторически предлагались различные «информационные критерии», которые пытались исправить смещение максимальной вероятности путем добавления штрафного члена, чтобы компенсировать чрезмерную подгонку более сложных моделей.

— стр. 33, Распознавание образов и машинное обучение, 2006 г.

Преимущество вероятностных методов выбора модели заключается в том, что набор тестовых данных не требуется, а это означает, что все данные могут использоваться для соответствия модели, а окончательная модель, которая будет использоваться для прогнозирования в области, может быть оценена напрямую.

Ограничение вероятностных методов выбора модели состоит в том, что одна и та же общая статистика не может быть рассчитана для ряда моделей разных типов.Вместо этого метрика должна быть тщательно выведена для каждой модели.

Следует отметить, что статистика AIC предназначена для заранее запланированных сравнений между моделями (в отличие от сравнения многих моделей во время автоматического поиска).

— стр. 493, Прикладное прогнозное моделирование, 2013 г.

Еще одним ограничением этих методов выбора является то, что они не принимают во внимание неопределенность модели.

Однако такие критерии не принимают во внимание неопределенность параметров модели, и на практике они склонны отдавать предпочтение слишком простым моделям.

— стр. 33, Распознавание образов и машинное обучение, 2006 г.

Существует три статистических подхода к оценке того, насколько хорошо данная модель соответствует набору данных и насколько она сложна. И можно показать, что каждое из них эквивалентно или пропорционально друг другу, хотя каждый был получен из разных рамок или области исследования.

Это:

• Информационный критерий Акаике (AIC). Получено из частотной вероятности.
• Байесовский информационный критерий (BIC).Получено из байесовской вероятности.
• Минимальная длина описания (MDL). На основе теории информации.

Каждая статистика может быть рассчитана с использованием логарифма правдоподобия для модели и данных. Логарифмическое правдоподобие исходит из оценки максимального правдоподобия, метода поиска или оптимизации параметров модели в ответ на набор обучающих данных.

При оценке максимального правдоподобия мы хотим максимизировать условную вероятность наблюдения данных ( X ) при заданном распределении вероятностей и его параметрах ( theta ), формально заявленных как:

Где X — это, по сути, совместное распределение вероятностей всех наблюдений из проблемной области от 1 до n.

• P (x1, x2, x3,…, xn; theta)

Совместное распределение вероятностей может быть переформулировано как произведение условной вероятности для наблюдения каждого примера с учетом параметров распределения. Умножение множества малых вероятностей может быть нестабильным; как таковой, эту проблему принято переформулировать как сумму условной вероятности в натуральном логарифме.

• сумма от i до n log (P (xi; theta))

Учитывая частое использование журнала в функции правдоподобия, его обычно называют функцией логарифма правдоподобия.

Функция логарифма правдоподобия для общих задач прогнозного моделирования включает среднеквадратичную ошибку для регрессии (например, линейной регрессии) и логарифмические потери (двоичная кросс-энтропия) для двоичной классификации (например, логистической регрессии).

Мы более подробно рассмотрим каждую из трех статистических данных, AIC, BIC и MDL, в следующих разделах.

Информационный критерий Акаике

Информационный критерий Акаике, сокращенно AIC, — это метод оценки и выбора модели.

Он назван в честь разработчика метода, Хиротугу Акаике, и может быть продемонстрирован как имеющий основу в теории информации и частотных выводах.

Это получено из частотной структуры и не может быть интерпретировано как приближение к предельному правдоподобию.

— стр. 162, Машинное обучение: вероятностная перспектива, 2012 г.

Статистика AIC определяется для логистической регрессии следующим образом (взято из «Элементов статистического обучения»):

• AIC = -2 / N * LL + 2 * k / N

Где N — количество примеров в наборе обучающих данных, LL — логарифмическая вероятность модели в наборе обучающих данных, а k — количество параметров в модели.

Оценка, как определено выше, сведена к минимуму, например выбирается модель с самым низким AIC.

Чтобы использовать AIC для выбора модели, мы просто выбираем модель, дающую наименьший AIC из множества рассмотренных моделей.

— стр. 231, Элементы статистического обучения, 2016 г.

По сравнению с методом BIC (ниже), статистика AIC меньше штрафует сложные модели, что означает, что он может уделять больше внимания производительности модели в наборе обучающих данных и, в свою очередь, выбирать более сложные модели.

Мы видим, что штраф для AIC меньше, чем для BIC. Это заставляет AIC выбирать более сложные модели.

— стр. 162, Машинное обучение: вероятностная перспектива, 2012 г.

Байесовский информационный критерий

Байесовский информационный критерий, или сокращенно BIC, — это метод оценки и выбора модели.

Он назван в честь области исследования, из которой он был получен: байесовская вероятность и вывод. Как и AIC, он подходит для моделей, соответствующих структуре оценки максимального правдоподобия.

Статистика BIC рассчитывается для логистической регрессии следующим образом (взято из «Элементов статистического обучения»):

• BIC = -2 * LL + log (N) * k

Где log () имеет основание e, называемое натуральным логарифмом, LL — логарифмическая вероятность модели, N — количество примеров в наборе обучающих данных, а k — это число. параметров в модели.

Оценка, как определено выше, сведена к минимуму, e.грамм. выбирается модель с самым низким BIC.

Рассчитанное количество отличается от AIC, хотя может быть показано, что оно пропорционально AIC. В отличие от AIC, BIC больше наказывает модель за ее сложность, а это означает, что более сложные модели будут иметь худшую (большую) оценку и, в свою очередь, с меньшей вероятностью будут выбраны.

Обратите внимание, что по сравнению с AIC […], это более серьезно снижает сложность модели.

— стр. 217, Распознавание образов и машинное обучение, 2006 г.

Важно отметить, что вывод BIC в рамках байесовской вероятностной структуры означает, что если выбор моделей-кандидатов включает истинную модель для набора данных, то вероятность того, что BIC выберет истинную модель, увеличивается с размером обучающего набора данных. Этого нельзя сказать о рейтинге AIC.

… учитывая семейство моделей, включая истинную модель, вероятность того, что BIC выберет правильную модель, приближается к единице, поскольку размер выборки N -> бесконечность.

— стр. 235, Элементы статистического обучения, 2016 г.

Обратной стороной BIC является то, что для небольших и менее репрезентативных обучающих наборов данных более вероятно выбрать слишком простые модели.

Минимальная длина описания

Минимальная длина описания, или сокращенно MDL, — это метод оценки и выбора модели.

Он назван в честь области исследований, из которой он был получен, а именно теории информации.

Теория информации связана с представлением и передачей информации по зашумленному каналу и, как таковая, измеряет такие величины, как энтропия, которая представляет собой среднее количество битов, необходимых для представления события из случайной величины или распределения вероятностей.

С точки зрения теории информации, мы можем захотеть передать как прогнозы (или, точнее, их распределения вероятностей), так и модель, используемую для их генерации. Как прогнозируемая целевая переменная, так и модель могут быть описаны с точки зрения количества битов, необходимых для их передачи по зашумленному каналу.

Минимальная длина описания — это минимальное количество битов или минимум суммы количества битов, необходимых для представления данных и модели.

Принцип минимальной длины описания (MDL) рекомендует выбирать гипотезу, которая минимизирует сумму этих двух длин описания.

— стр. 173, Машинное обучение, 1997.

Статистика MDL рассчитывается следующим образом (взято из «Машинного обучения»):

Где h — модель, D — прогноз, сделанный моделью, L (h), — количество битов, необходимых для представления модели, а L (D | h) — количество биты, необходимые для представления прогнозов модели в наборе обучающих данных.

Оценка, как определено выше, сведена к минимуму, например выбирается модель с наименьшим MDL.

Количество битов, необходимых для кодирования ( D | h ), и количество битов, необходимых для кодирования ( h ), можно вычислить как отрицательную логарифмическую вероятность; например (взято из «Элементов статистического обучения»):

• MDL = -log (P (theta)) — log (P (y | X, theta))

Или отрицательная логарифмическая вероятность параметров модели ( theta ) и отрицательная логарифмическая вероятность целевых значений ( y ) с учетом входных значений ( X ) и параметров модели ( theta ) .

Это желание минимизировать кодирование модели и ее прогнозов связано с идеей бритвы Оккама, которая ищет простейшее (наименее сложное) объяснение: в этом контексте наименее сложная модель, которая прогнозирует целевую переменную.

Принцип MDL исходит из того, что лучшая теория для массива данных — это та, которая минимизирует размер теории плюс количество информации, необходимой для определения исключений относительно теории…

— стр. 198, Интеллектуальный анализ данных: практические инструменты и методы машинного обучения, 4-е издание, 2016 г.

Расчет MDL очень похож на BIC и в некоторых ситуациях может быть эквивалентен.

Следовательно, критерий BIC, полученный как приближение к логарифмической апостериорной вероятности, также можно рассматривать как средство для (приблизительного) выбора модели по минимальной длине описания.

— стр. 236, Элементы статистического обучения, 2016 г.

Рабочий пример для линейной регрессии

Мы можем произвести расчет бетона AIC и BIC на отработанном примере.

В этом разделе мы воспользуемся тестовой задачей и построим модель линейной регрессии, а затем оценим модель, используя показатели AIC и BIC.

Важно отметить, что конкретная функциональная форма AIC и BIC для модели линейной регрессии была получена ранее, что делает пример относительно простым. При адаптации этих примеров для ваших собственных алгоритмов важно либо найти соответствующий вывод расчета для вашей модели и задачи прогнозирования, либо самостоятельно провести расчет.

В этом примере мы будем использовать задачу тестовой регрессии, предоставляемую функцией scikit-learn make_regression (). Задача будет иметь две входные переменные и потребовать предсказания целевого числового значения.

…
# создать набор данных
X, y = make_regression (n_samples = 100, n_features = 2, noise = 0,1)
# определить и подогнать модель ко всем данным

Мы подгоним модель LinearRegression () непосредственно ко всему набору данных.

…
# определить и подогнать модель ко всем данным
model = LinearRegression ()
model.fit (X, y)

После подбора мы можем сообщить количество параметров в модели, которое, учитывая определение проблемы, мы ожидаем равным трем (два коэффициента и одно пересечение).

…
# количество параметров
num_params = len (model.coef_) + 1
print (‘Количество параметров:% d’% (num_params))

Можно показать, что функция правдоподобия для модели линейной регрессии идентична функции наименьших квадратов; следовательно, мы можем оценить максимальную правдоподобность модели с помощью показателя среднеквадратичной ошибки.

Во-первых, модель может использоваться для оценки результата для каждого примера в наборе обучающих данных, затем функция scikit-learn mean_squared_error () может использоваться для вычисления среднеквадратичной ошибки для модели.

…
# предсказать обучающую выборку
yhat = model.predict (X)
# вычисляем ошибку
mse = mean_squared_error (y, yhat)
print (‘MSE:% .3f’% mse)

Объединяя все это вместе, полный пример определения набора данных, подгонки модели и отчета о количестве параметров и оценке максимального правдоподобия модели приведен ниже.

# создать тестовый набор данных и подобрать модель линейной регрессии
из sklearn.datasets импортировать make_regression
из склеарна.linear_model импорт LinearRegression
из sklearn.metrics import mean_squared_error
# создать набор данных
X, y = make_regression (n_samples = 100, n_features = 2, noise = 0,1)
# определить и подогнать модель ко всем данным
model = LinearRegression ()
model.fit (X, y)
# количество параметров
num_params = len (model.coef_) + 1
print (‘Количество параметров:% d’% (num_params))
# предсказать обучающую выборку
yhat = model.predict (X)
# вычисляем ошибку
mse = mean_squared_error (y, yhat)
print (‘MSE:%.3f ‘% mse)

Примечание : Ваши результаты могут отличаться из-за стохастической природы алгоритма или процедуры оценки или различий в числовой точности. Попробуйте запустить пример несколько раз и сравните средний результат.

При выполнении примера сначала отображается количество параметров модели равное 3, как мы и ожидали, а затем MSE составляет около 0,01.

Количество параметров: 3
MSE: 0,010

Затем мы можем адаптировать пример для расчета AIC для модели.

Пропуская вывод, расчет AIC для обычной модели линейной регрессии методом наименьших квадратов может быть рассчитан следующим образом (взято из «Новый взгляд на статистическую модель идентификации», 1974 г.):

Где n — количество примеров в наборе обучающих данных, LL — логарифмическая вероятность для модели с использованием натурального логарифма (например,грамм. журнал MSE), а k — количество параметров в модели.

Функция calculate_aic () ниже реализует это, принимая в качестве аргументов n , грубую среднеквадратичную ошибку ( mse ) и k .

# вычислить aic для регрессии
def calculate_aic (n, mse, num_params):
aic = n * журнал (mse) + 2 * num_params
вернуть aic

Затем пример можно обновить, чтобы использовать эту новую функцию и вычислить AIC для модели.

Полный пример приведен ниже.

# вычислить информационный критерий акаике для модели линейной регрессии
из журнала импорта математики
из sklearn.datasets импортировать make_regression
из sklearn.linear_model import LinearRegression
из sklearn.metrics import mean_squared_error

# вычислить aic для регрессии
def calculate_aic (n, mse, num_params):
aic = n * журнал (mse) + 2 * num_params
вернуть aic

# создать набор данных
X, y = make_regression (n_samples = 100, n_features = 2, noise = 0.1)
# определить и подогнать модель ко всем данным
model = LinearRegression ()
model.fit (X, y)
# количество параметров
num_params = len (model.coef_) + 1
print (‘Количество параметров:% d’% (num_params))
# предсказать обучающую выборку
yhat = model.predict (X)
# вычисляем ошибку
mse = mean_squared_error (y, yhat)
print (‘MSE:% .3f’% mse)
# вычисляем aic
aic = calculate_aic (len (y), mse, num_params)
print (‘AIC:% .3f’% aic)

Выполнение примера сообщает количество параметров и MSE, как и раньше, а затем сообщает AIC.

Примечание : Ваши результаты могут отличаться из-за стохастической природы алгоритма или процедуры оценки или различий в числовой точности. Попробуйте запустить пример несколько раз и сравните средний результат.

В этом случае сообщается, что AIC имеет значение около -451,616. Это значение можно минимизировать, чтобы выбрать лучшие модели.

Количество параметров: 3
MSE: 0,010
АИК: -451,616

Мы также можем изучить тот же пример с расчетом BIC вместо AIC.

Пропуская вывод, расчет BIC для обычной модели линейной регрессии методом наименьших квадратов можно рассчитать следующим образом (взято отсюда):

• BIC = n * LL + k * log (n)

Где n — количество примеров в наборе обучающих данных, LL — логарифм правдоподобия для модели с использованием натурального логарифма (например,грамм. log средней квадратичной ошибки), а k — количество параметров в модели, а log () — натуральный логарифм.

Функция calculate_bic () ниже реализует это, принимая в качестве аргументов n , грубую среднеквадратичную ошибку ( mse ) и k .

# вычислить bic для регрессии
def calculate_bic (n, mse, num_params):
bic = n * журнал (mse) + num_params * log (n)
вернуть bic

Затем пример можно обновить, чтобы использовать эту новую функцию и вычислить BIC для модели.

Полный пример приведен ниже.

# вычислить байесовский информационный критерий для модели линейной регрессии
из журнала импорта математики
из sklearn.datasets импортировать make_regression
из sklearn.linear_model import LinearRegression
из sklearn.metrics import mean_squared_error

# вычислить bic для регрессии
def calculate_bic (n, mse, num_params):
bic = n * журнал (mse) + num_params * log (n)
вернуть bic

# создать набор данных
X, y = make_regression (n_samples = 100, n_features = 2, noise = 0.1)
# определить и подогнать модель ко всем данным
model = LinearRegression ()
model.fit (X, y)
# количество параметров
num_params = len (model.coef_) + 1
print (‘Количество параметров:% d’% (num_params))
# предсказать обучающую выборку
yhat = model.predict (X)
# вычисляем ошибку
mse = mean_squared_error (y, yhat)
print (‘MSE:% .3f’% mse)
# вычисляем bic
bic = calculate_bic (len (y), mse, num_params)
print (‘BIC:% .3f’% bic)

При выполнении примера сообщается количество параметров и MSE, как и раньше, а затем сообщается BIC.

Примечание : Ваши результаты могут отличаться из-за стохастической природы алгоритма или процедуры оценки или различий в числовой точности. Попробуйте запустить пример несколько раз и сравните средний результат.

В этом случае сообщается, что BIC имеет значение около -450,020, что очень близко к значению AIC, равному -451,616. Опять же, это значение можно минимизировать, чтобы выбрать лучшие модели.

Количество параметров: 3
MSE: 0.010
БИК: -450.020

Дополнительная литература

Этот раздел предоставляет дополнительные ресурсы по теме, если вы хотите углубиться.

Книги

• Глава 7 Оценка и выбор модели, Элементы статистического обучения, 2016.
• Раздел 1.3 Выбор модели, распознавание образов и машинное обучение, 2006 г.
• Раздел 4.4.1 Сравнение моделей и BIC, Распознавание образов и машинное обучение, 2006.
• Раздел 6.6 Принцип минимальной длины описания, Машинное обучение, 1997.
• Раздел 5.3.2.4 Приближение BIC к журналу предельного правдоподобия, Машинное обучение: вероятностная перспектива, 2012.
• Прикладное прогнозное моделирование, 2013 г.
• Раздел 28.3 Минимальная длина описания (MDL), Теория информации, алгоритмы вывода и обучения, 2003.
• Раздел 5.10 Принцип MDL, Интеллектуальный анализ данных: практические инструменты и методы машинного обучения, 4-е издание, 2016 г.

Документы

API

Статьи

Сводка

В этом посте вы обнаружили вероятностную статистику для выбора модели машинного обучения.

В частности, вы выучили:

• Выбор модели — это проблема выбора одной из множества моделей-кандидатов.
• Akaike и байесовский информационный критерий — это два способа оценки модели на основе ее логарифмической вероятности и сложности.
• Minimum Description Length предоставляет еще один метод оценки из теории информации, который может быть эквивалентен BIC.

Есть вопросы?
Задайте свои вопросы в комментариях ниже, и я постараюсь ответить.

Получите представление о вероятности машинного обучения!

Развивайте свое понимание вероятности

… всего несколькими строками кода Python

Узнайте, как это сделать, в моей новой электронной книге:
Probability for Machine Learning

Он предоставляет руководств для самообучения и сквозных проектов по:
Теорема Байеса , Байесовская оптимизация , Распределения , Максимальное правдоподобие , Кросс-энтропия , Калибровка моделей
и многое другое…

Наконец-то используйте неопределенность в своих проектах

Пропустите академики. Только результаты.

Посмотрите, что внутри

Как строится IBAN?

IBAN может содержать не более 34 буквенно-цифровых символов. В Греции стандартная длина составляет 27 буквенно-цифровых символов:

.

• Первые два буквенных символа определяют страну, в которой открыт счет (GR для Греции).
• следующие две цифры — это контрольные цифры.Они проверяют полный IBAN и
• последняя часть IBAN — это базовый номер банковского счета или BBAN, который в большинстве случаев является номером, идентифицирующим банк, филиал и номер счета клиента1.

В Греции основной номер банковского счета:

1. Три (3) цифры для кода банка
2. Четыре (4) цифры для кода отделения
3. Шестнадцать (16) цифр для номера счета клиента *.

* Если количество цифр в номере счета меньше 16, банк должен заполнить его нулями, помещенными в начало счета.

Как представлен IBAN?

IBAN можно использовать в электронной и печатной среде. Печатное представление IBAN такое же, как и в электронном формате, за исключением того, что при печати пробел вставляется после каждой группы из четырех символов.

Примеры

ΙΒΑΝ Подтверждение

Чтобы предотвратить неправильный ввод, Компании могут внедрить в свои информационные системы алгоритм проверки контрольных цифр IBAN.

SWIFT / BIC

Байесовский информационный критерий (BIC) / критерий Шварца

Байесовская статистика>

Байесовский информационный критерий (BIC) — это индекс, используемый в байесовской статистике для выбора между двумя или более альтернативными моделями .

BIC также известен как информационный критерий Schwarz (сокращенно.SIC) или критериев информации Шварца-Байеса . Он был опубликован в 1978 году в статье Гидеона Э. Шварца и тесно связан с информационным критерием Акаике (AIC), который был официально опубликован в 1974 году.

Определение байесовского информационного критерия / критерия Шварца

Байесовский информационный критерий (BIC) определяется как

k log (n) — 2log (L (θ̂)).

Здесь n — размер выборки; количество наблюдений или количество точек данных, с которыми вы работаете.k — это количество параметров, которые оценивает ваша модель, а θ — это набор всех параметров.

L (θ̂) представляет собой вероятность протестированной модели с учетом ваших данных при оценке при максимальных значениях правдоподобия θ. Вы могли бы назвать это вероятностью модели, учитывая, что все соответствует их наиболее благоприятному положению.

Другой способ понять L (θ̂) — это вероятность получения данных, которые у вас есть, если предположить, что тестируемая модель задана.

Сравнение моделей

Сравнение моделей с байесовским информационным критерием просто включает в себя вычисление BIC для каждой модели. Модель с самым низким BIC считается лучшей, и ее можно записать в формате BIC ^* (или SIC ^* , если вы используете это имя и сокращение).

Мы также можем рассчитать Δ BIC; различие между конкретной моделью и «лучшей» моделью с самым низким BIC, и использовать ее в качестве аргумента против другой модели. Δ BIC — это просто BIC _модель — BIC ^* , где BIC * — лучшая модель.

Если Δ BIC меньше 2, это считается «едва стоящим упоминания» в качестве аргумента либо в пользу лучшей теории, либо против альтернативной.Преимущество, которое он дает нашей лучшей модели, слишком мало, чтобы быть значимым. Но если Δ BIC находится между 2 и 6, можно сказать, что свидетельство против другой модели является положительным; т.е. у нас есть веские аргументы в пользу нашей «лучшей модели». Если оно составляет от 6 до 10, значит, есть веские доказательства в пользу лучшей модели и против более слабой. Δ BIC больше десяти означает, что доказательства в пользу нашей лучшей модели по сравнению с альтернативной действительно очень сильны.

Пример

Предположим, у вас есть набор данных с 50 точками наблюдения, а Модель 1 оценивает 3 параметра.Модель 2 оценивает 4 параметра. Допустим, логарифм вашей максимальной вероятности для модели 1 составляет a ; а для модели 2 это 2 a . Используя формулу k log (n) — 2log (L (θ)):

Расчет SIC по этим данным дает:

• Модель 1: 3log (50) — 2a = 5,1 — 2a
• Модель 2: 4log (50) — 4a = 6,8 — 4a

Итак, ΔBIC составляет 1,7 — 2a.

Поскольку доказательства, которые дает нам байесовский информационный критерий для модели 1, «заслуживают упоминания» только в том случае, если 1.7 — 2a> 2, мы можем требовать окончательных результатов, только если -2a> 0,3; то есть <-0,15.

Ссылки

Клаескинс, Г. и Хкорт, Н. (2008). Выбор модели и усреднение модели (Кембриджская серия по статистической и вероятностной математике) 1-е издание. Издательство Кембриджского университета.
Fabozzi, Focardi, Rachev & Arshanapalli. Основы финансовой эконометрики: инструменты, концепции и приложения для управления активами. Приложение E: Критерий выбора модели: AIC и BIC.Получено с http://onlinelibrary.wiley.com/store/10.1002/9781118856406.app5/asset/app5.pdf;jsessionid=A6726BA5AE1AD2A5AF007FFF78528249.f03t01?v=1&t=je8jr983&sefc845d09eca3, March8c8459ec89909ec8c8459ec8ec8ec8a09ec8ec8ec8a09ec8 STAT 705 Lecture Notes: выбор модели
Получено с http://www.stat.cmu.edu/~larry/=stat705/Lecture16.pdf, 1 марта 2018 г.

————————————————— —————————-

Нужна помощь с домашним заданием или контрольным вопросом? С помощью Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .

Как FindDistribution вычисляет BIC и AIC?

Не похоже, что стандартное определение AIC используется в FindDistribution . Обычная формула с
$ n $ наблюдений и
$ k $ параметры
$ AIC = -2 \ log L + 2 тыс. $. Но FindDistribution , похоже, использует
$ AIC = 2 \ log L — 2k / (n-k-1) $.

Вот «доказательство» того, что использует FindDistribution . (Это работает, если не найдено MixtureDistribution с более чем двумя распределениями.)

Задайте размер выборки и получите случайную выборку:

 n = 100;
data = RandomVariate [Exponential [1], n];
 

Найдите наиболее подходящие распределения и соберите значения AIC и LogLikelihood :

 nbest = 5;
fd = FindDistribution [данные, nbest, {"AIC", "LogLikelihood"}]
(* {{ExponentialDistribution [1.07497], {-1.83436, -0.
6}},
{MixtureDistribution [{0,72248, 0,27752}, {GammaDistribution [1,2916, 0,369832], UniformDistribution [{0,0177466, 3,77159}]}], {-1,75598, -0,824797}},
{MixtureDistribution [{0.765586, 0.234414}, {GammaDistribution [1.3553, 0.342329], NormalDistribution [2.45319, 0.808439]}], {- 1.78878, -0.841199}},
{LogNormalDistribution [-0.708397,1.24473], {-1.84787, -0.
9}},
{WeibullDistribution [0,92819,0,897149], {-1,85254, -0,
1}}} *)
 
 Найти
 $ k $ (количество параметров):
 k = StringCount [Таблица [ToString [fd [[i, 1]]], {i, nbest}], «,»] + 1;
(* {1,6,6,2,2} *)
nMixtures = StringCount [Таблица [ToString [fd [[i, 1]]], {i, nbest}], "MixtureDistribution"]
(* {0,1,1,0,0} *)
k = k - n Смеси
(* {1,5,5,2,2} *)
 
 Извлеките значения  LogLikelihood  и  AIC  и покажите значения  AIC  из формулы, используемой  FindDistribution :
 logL = Таблица [fd [[i, 2, 2]], {i, nbest}]
(* {-0.
63208709088`, -0.8247971259593575`, -0.8411993739988386`, -0.
8
0027`, -0.
064931`} *)
aic = Таблица [fd [[i, 2, 1]], {i, nbest}]
(* {-1.8343608050071236`, -1.7559772306421193`, -1.7887817267210813`, -1.847874
2116`, -1.8525384132295681`} *)
2 logL - 2 к / (п - к - 1)
(* {-1.8343608050071238`, -1.7559772306421193`, -1.7887817267210815`, -1.847874
2116`, -1.8525384132295681`} *)
 
 Похоже, что использованная формула неверна и что это комбинация
 $ AIC $ и
 $ AIC_c $ как
 $ AIC_c = -2 \ log L + 2 k n / (n-k-1) $.
 Mobilefish.com — конвертер BBAN в IBAN 
Этот инструмент покрывает от 4000 базовых номеров банковских счетов (BBAN) до международных номеров банковских счетов (IBAN).
 Этот инструмент также проверяет формат основных номеров банковских счетов, но не проверяет, существуют ли BBAN на самом деле.
 К номерам счетов в голландских банках применяются дополнительные проверки, так называемый тест на одиннадцать.
 BBAN состоит из 30 буквенно-цифровых символов (A – Z, 0–9), имеет фиксированную длину для каждой страны и включает идентификационный код.
 банка / филиала, обслуживающего счет в фиксированных позициях в BBAN, а также номер счета клиента в фиксированных позициях в BBAN.Базовые номера банковских счетов сильно различаются в разных странах, но имеют некоторые общие характеристики. Обычно он состоит из 2-6 частей.
   BBAN пример воображаемой страны NN  :
 Х
 м
 Ф
 Я
 S
 H
 4
 3
 9
 0
 0
 9
 3
 4
 0
 2
 3
 4
 5
 9
 9
 0
 7
 А
 где:
 Проверка 1 (1! А) 
 Лишь в нескольких странах используются контрольные цифры «check 1».
 В этом примере BBAN первый символ представляет символ «проверка 1»: 
  X 
 Идентификатор банка (5! А) 
 Идентификационный код поставщика платежных услуг (банка). 
 В этом примере BBAN следующие 5 буквенных символов представляют «идентификатор банка»: 
  MFISH 
 Идентификатор отделения (3! N) 
 Идентификационный код организационной единицы поставщика платежных услуг (филиала). 
 В этом примере BBAN следующие 3 цифровых символа представляют «идентификатор ветки»: 
  439 
 Проверка 2 (2! N) 
 Лишь в нескольких странах используются контрольные цифры «check 2».
 В этом примере BBAN следующие 2 цифровых символа представляют цифры «check 2»: 
  00 
 Номер счета (11! N) 
 Идентификационный номер клиента банка (номер счета). 
 В этом примере BBAN следующие 11 цифровых символов представляют «номер счета»: 
  93402345990 
 Проверка 3 (2! C) 
 Лишь в некоторых странах используются контрольные цифры «контрольной 3». 
 В этом примере BBAN следующие два буквенно-цифровых символа представляют символы «проверки 3»: 
  7A 
Точная структура BBAN зависит от страны и может быть найдена в таблице ниже:
 Ввод конвертера BBAN в IBAN: 
 Вывод конвертера BBAN в IBAN: 
  Преобразованный BBAN в IBAN 
 Нет данных.
  Неверный BBAN 
 Нет данных.
 Калькулятор логарифма правдоподобия и размера эффекта 
 Обратите внимание, что значение c соответствует количеству слов в корпусе.
 один, а ‘d’ соответствует количеству слов во втором корпусе (N
 значения). Значения ‘a’ и ‘b’ называются наблюдаемыми значениями (O),
 тогда как нам нужно рассчитать ожидаемые значения (E) в соответствии с
 следующая формула:
 В нашем случае N1 = c, а N2 = d.Итак, для этого слова E1 = c * (a + b) / (c + d)
 и E2 = d * (a + b) / (c + d). Расчет ожидаемых значений занимает
 учитывать размер двух корпусов, поэтому нам не нужно
 нормализовать цифры перед применением формулы. Тогда мы можем
 рассчитайте значение логарифма правдоподобия по этой формуле:
 Это равносильно вычислению логарифма правдоподобия G2 следующим образом:
G2 = 2 * ((a * ln (a / E1)) + (b * ln (b / E2)))
  Примечание 1:  (спасибо Stefan Th. Gries) Форма логарифмической вероятности
 расчет, который я использую, взят из исследования Рида и Кресси, цитируемого в
 Райсон и Гарсайд (2000), а не форма, полученная у Даннинга (1993).
  Примечание 2:  (спасибо Крису Брю)
 Чтобы сформировать логарифмическую вероятность, мы вычисляем сумму по членам формы
 х * ln (х / Е). Для строго положительного x эти члены легко вычислить,
 в то время как, если x равен нулю, ln (x / E) будет отрицательной бесконечностью.
 Однако предел
 x * ln (x), когда x стремится к нулю, все еще равно нулю, поэтому при суммировании мы можем просто
 игнорировать ячейки, где x = 0.
 Вычисление ln (0) возвращает ошибку, например, в
 MSExcel и библиотека C-maths.
 Чем выше значение G2, тем значительнее разница между
 две оценки частоты.Для этих таблиц G2 3,8 или выше соответствует
 значимо на уровне p
 95-й процентиль; 5% уровень; p 99-й процентиль; Уровень 1%; p 99,9-й процентиль; Уровень 0,1%; p 99,99-й процентиль; Уровень 0,01%; п
 Расчет величины эффекта 
 Наряду с мерой журнала правдоподобия на этой странице реализованы следующие меры размера эффекта:
 % DIFF  — см. Габриелатос и Марчи (2012) 
 Костас также предоставил FAQ с более подробной информацией
  Байесовский фактор (BIC)  — см. Wilson (2013) 
 Вы можете интерпретировать приблизительный байесовский фактор как степень доказательства против нулевой гипотезы следующим образом: 
 0-2: не стоит больше, чем просто упоминание 
 2-6 : положительные доказательства против H0 
 6-10: сильные доказательства против H0 
> 10: очень сильные доказательства против H0 
 Для отрицательных оценок шкала читается как «в пользу» вместо «против» (Уилсон, личное сообщение).
  Размер эффекта для логарифма правдоподобия (ELL)  — см. Johnston et al (2006). 
 ELL варьируется от 0 до 1 (включительно). Johnston et al. говорят, что «интерпретация проста как пропорция максимального расхождения между
 соблюдаемые и ожидаемые пропорции ».
  Относительный риск  — см. Ссылки ниже
  Log Ratio  — см. Блог Эндрю Харди CASS, чтобы узнать, как это интерпретировать.
 
 Обратите внимание, что если какое-либо слово имеет нулевую частоту, автоматически применяется небольшая корректировка (0.5 наблюдаемая частота
 который затем нормализуется), чтобы избежать деления на ноль ошибок.
  Коэффициент шансов  — см. Ссылки ниже
 Дополнительная литература 
Для подробного сравнения статистики логарифма правдоподобия и хи-квадрат см. 
  Rayson P., Berridge D. and Francis B.  (2004).
 Расширение правила Кохрана для сравнения частот слов в корпусах.
 В  Том II Purnelle G., Fairon C., Dister A. (eds.)
 Le poids des mots: Труды 7-й Международной конференции по
 Статистический анализ текстовых данных
 (JADT 2004), Лувен-ла-Нев, Бельгия, 10-12 марта 2004 г. ,
 Прессы Universitaires de Louvain, стр.926 — 936. ISBN 2-930344-50-4.
 Тест логарифмического правдоподобия можно использовать для сравнения корпусов. См. 
  Rayson, P. and Garside, R.  (2000).
 Сравнение корпусов с использованием частотного профилирования.
 В материалах семинара  г.
 Сравнивая корпуса,
 проводится в рамках 38-го ежегодного собрания Ассоциации компьютерной лингвистики
 (ACL 2000) .
 1-8 октября 2000 г., Гонконг, стр. 1-6.
 Более подробный обзор различных статистических данных см .: 
  Rayson, P. (2003).
 Матрица: статистический метод и программный инструмент для лингвистического анализа с помощью
 сравнение корпусов.
  к.э.н. диссертация , Ланкастерский университет.
 Чтобы узнать больше об использовании логарифма правдоподобия для сравнений на уровне тегов, см .: 
  Rayson, P.  (2008).
 От ключевых слов до ключевых семантических областей.
  Международный журнал корпусной лингвистики .
 13: 4 с. 519-549.
 DOI: 10.1075 / ijcl.13.4.06ray
 Калькулятор распределения хи-квадрат (Stat Trek)
 позволяет легко вычислить
 кумулятивные вероятности, основанные на статистике хи-квадрат.
 В Институте фонетических наук в Амстердаме есть аналогичный калькулятор.
 Также см.  Dunning, Ted.  (1993).
 Точные методы статистики неожиданностей и совпадений.
  Компьютерная лингвистика , Том 19, номер 1, стр. 61-74.
 (pdf)
 Эндрю Харди создал
 система проверки значимости
 который вычисляет хи-квадрат, логарифм правдоподобия и точный критерий Фишера.
 для таблиц непредвиденных обстоятельств с использованием R.
 В корпусной лингвистике и других областях наблюдается растущее движение.
 (е.грамм. Психология)
 отойти от проверки нулевых гипотез и p-значений,
 и для расчета мер величины эффекта, а также значений значимости.
 Чтобы обсудить эти меры и зачем они нам нужны,
 см. следующие ресурсы,
 презентации и публикации:
 CEP932 размер эффекта содержание
 в котором обсуждаются такие меры, как d Коэна, коэффициент корреляции r Пирсона и отношение шансов.
 Вацлав Брезина (2014) Размеры эффекта в корпусной лингвистике:
 ключевые слова, словосочетания и диахроническое сравнение.Представлено на конференции ICAME 2014, Ноттингемский университет.
 [Вацлав использует D Коэна как меру величины эффекта.]
 Величина эффекта для теста хи-квадрат
 который описывает такие меры, как Phi, Cramer’s V,
 Соотношение шансов и
 Относительный риск
 Статистика для объяснения психологии
 Проверка нулевой гипотезы и размеры эффекта, которые, например,
 «Если небольшая разница между средними значениями двух групп не имеет значения, когда я тестирую 100 человек, должен ли я внезапно восхищаться точно такой же разницей, если после тестирования 1000 человек я обнаружил, что теперь она значительна?»
 Gries, Stefan Th.(2014)
 Таблицы частот, размеры эффектов и исследования.
 В Дилане Глинне и Юстине Робинсон (ред.), Методы Корпуса для семантики: количественные исследования в многозначности и синонимии, 365-389. Амстердам и Филадельфия: Джон Бенджаминс.
 [В этой статье Стефан использует меры размера эффекта Phi, отношение шансов для таблиц 2 x 2 и V Крамера для больших таблиц r-by-c.]
 Коэффициент логарифма Эндрю Харди
 который фактически является двоичным журналом относительного риска и может применяться только к
 2 х 2 стола вместе с коэффициентом шансов.
 Джонстон, Дж. Э., Берри, К. Дж. и Mielke, P.W. (2006)
 Меры величины эффекта для критериев согласия и критерия согласия.
 Перцептивные и моторные навыки: Том 103, выпуск, стр. 412-414.
 DOI: 10.2466 / pms.103.2.412-414
 [Это представляет меру размера эффекта, применимую к логарифмической вероятности.]
 Kuhberger A, Fritz A, Scherndl T (2014).
 Публикационная предвзятость в психологии: диагноз, основанный на корреляции между размером эффекта и размером выборки.
 PLoS ONE 9 (9): e105825. DOI: 10.1371 / journal.pone.0105825
 Джеффри Т. Лик и Роджер Д. Пэн (2015)
 Статистика: значения P — это лишь верхушка айсберга.
 Nature 520, 612 (30 апреля 2015 г.) doi: 10.1038 / 520612a
 [Этот документ призывает нас не сосредотачиваться только на статистике: «Статистики и люди, которых они учат и с которыми сотрудничают, должны прекратить споры о значениях P и не дать остальной части айсберга потопить науку».]
 Дональд Шарп (2015)
 Ваш критерий хи-квадрат статистически значим: что теперь?
 Практическая оценка, исследования и оценка.Volume 20, Number 8, апрель 2015.
 Блог Скотта Вайнгарта 2013 г.
 Друзья не позволяют друзьям вычислять p-значения (не понимая их полностью)
 Блог и статья Шона Уоллиса о
 Меры ассоциации для таблиц непредвиденных обстоятельств
 Камминг, Г. (2014)
 Новая статистика: почему и как.
 Психологическая наука. 25 (1), стр. 7-29.
 DOI: 10.1177 / 0956797613504966
 [Упоминает, что D Коэна широко используется, но имеет подводные камни.]
 Габриелатос, К. и Марчи, А. (2012)
 Ключевые слова: соответствующие показатели и практические вопросы.Международная конференция CADS 2012. Исследования дискурса с помощью корпуса: больше, чем сумма анализа дискурса и вычислений?, 13–14 сентября, Болонский университет, Италия.
 [Представляет показатель размера эффекта% DIFF, который, по мнению Костаса и Анны, следует применять к попарным сравнениям корпусов для расчета ключевости.]
 Gries, Stefan Th. (2005)
 Проверка значимости нулевой гипотезы частотности слов: продолжение Килгаррифа.
 Корпусная лингвистика и лингвистическая теория 1 (2). 277-294.
 [Стефан сравнивает хи-квадрат, p-значения, V Крамера, d Коэна и d *, а также
 Поправки Бонферрони и Холма для апостериорного тестирования.]
Есть ряд других работ, связанных с использованием проверки значимости,
 статистика ключевости и сравнение корпусов, например
 Килгаррифф (2005),
 Пако и Бестген (2009),
 Барон и др. (2009),
 Уилсон (2013)
 а также
 Lijffijt et al.
 Таблица для загрузки 
 Я сделал электронную таблицу, включающую расчет логарифмической вероятности и набор мер размера эффекта:
 SigEff.xlsx (последнее обновление 4 июля 2016 г.). Это будет полезно, если вы хотите рассчитать большой
 количество результатов из ранее существовавших наборов данных.Все размеры эффекта реализованы для случая 2 x 2, но только байесовский фактор и ELL реализованы для общего случая R x C,
 потому что% DIFF, относительный риск, коэффициент логарифма и коэффициент шансов применимы только для попарных сравнений.
Если у вас возникнут технические проблемы, свяжитесь с нами.
 Пол Райсон
 AHDB.DirectPaymentsCalculator 
 AHDB.DirectPaymentsCalculator
 Этот базовый инструмент можно использовать для простого расчета, как сокращение платежей BPS в Англии, которое должно начаться в 2021 году, повлияет на ваш фермерский бизнес.Просто введите сумму вашего платежа за 2020 год (2019, если не получен платеж за 2020 год), и калькулятор покажет, как могут выглядеть сокращения по сравнению с относительной общей суммой BPS, полученной вашим бизнесом в 2020 году. В настоящее время калькулятор учитывает платеж BPS только в его текущем форма и не принимает во внимание какое-либо внедрение ELM, а также существующие схемы платежей, такие как управление сельской местностью или новую платежную систему, которая должна быть развернута в течение сельскохозяйственного переходного периода.Для получения дополнительной информации о ELM и других схемах государственных платежей, которые должны заменить текущую структуру,.
 Для Северной Ирландии,
 Для Уэльса,
 Для Шотландии,
 Заметки
 В настоящее время у нас есть информация о сокращении только до 2024 года, другие годы рассчитаны линейным методом до 2028 года. Мы будем обновлять этот калькулятор по мере поступления дополнительной информации.
 Этот калькулятор в настоящее время применим только к сельскохозяйственным предприятиям, базирующимся в Англии: он будет обновлен, чтобы включить другие децентрализованные страны, как только необходимая информация станет доступной.
 Никакие данные, введенные в этот калькулятор, не будут сохранены
 Совет по развитию сельского хозяйства и садоводства стремится обеспечить, чтобы информация, содержащаяся в этом
 документ является точным на момент печати, в отношении него не дается никаких гарантий и, в максимальной степени, разрешенной законом,
 Совет по развитию сельского хозяйства и садоводства не несет ответственности за убытки, ущерб или травмы, какими бы причинами они ни были (в том числе
 вызванные небрежностью) или понесенные прямо или косвенно в отношении информации и мнений, содержащихся или опущенных в этом
 документ.
No related posts.